우리들의 T'SPACE

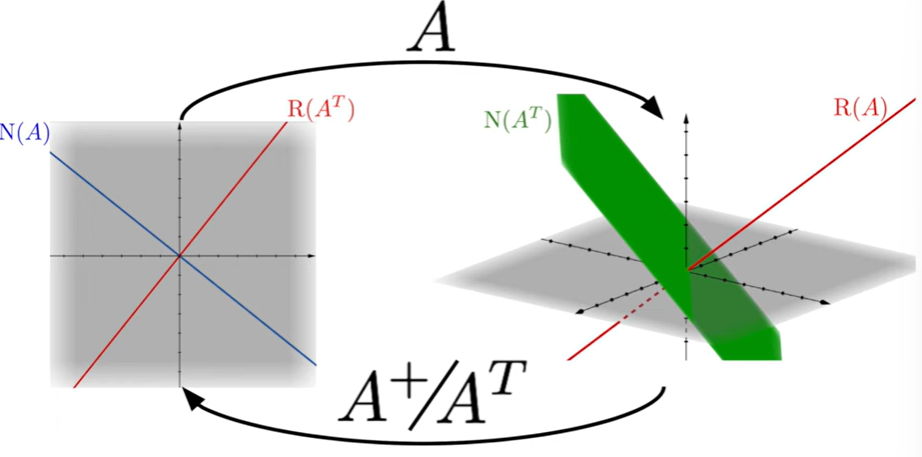
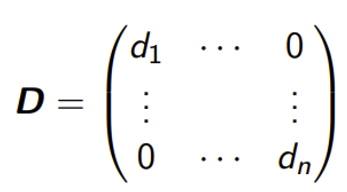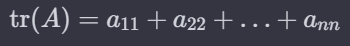처음 대학교 2학년때 선형 대수학을 배웠을 때가 생각난다 이 까지 진도를 나갔을 때 즘에는 종강이 한달도 남지 않은 여름 냄새가 풀풀한 1학기 말이였다 여름 열기에 안그래도 더운데 위에 이 4 Fundamental Subspace 그림은 전혀 도움을 주지 않았다... 어려워하는 학생들의 입장을 너무나 잘 알기에, 이번에 이해하는데 좀 도움을 주자고 한다 우선 부분공간은 뭘까? Subspace 부분공간(Subspace) 부분공간은 벡터 공간의 핵심 개념으로, 선형대수학에서 매우 중요한 역할을 합니다. 부분공간은 다음과 같은 특징을 가지고 있다: 영벡터의 포함: 부분공간에는 항상 영벡터(all-zero vector)가 포함되어 있습니다. 벡터 덧셈에 대한 폐쇄성: 부분공간의 두 벡터를 더하면 결과 벡터도 부..

대각 행렬은 위와 같이 i,j의 좌표가 같은 원소에만 값이 있는 행렬을 뜻 한다 쉽게말해 행렬에 죄측최상단 원소부터 대각선으로 내려오는 곳에 원소들만 있는 행렬이다 나머지는 0 그리고 그 원소들이 모두 1이면 Identity Matrix 항등 행렬이다 특징으로는 1) 대각행렬의 k승은 각 원소들을 각각 k승 한 것과 같다 2) 대각행렬의 역행렬은 각 원소들의 역수와 같다 3) determinent는 모든 원소들의 곱과 같다 4) Trace와 eigenvector(고유벡터)와의 관계에 의해 대각행렬의 각원소들은 그 대각행렬의 eigenvalue(고유값)이다 5) Symmetric, 대칭, 이다 https://tonnykang.tistory.com/96 eigenvalues & eigenvectors (고유..

일반적으로 고유값과 고유벡터를 배우면 위와 같은 식이 주어진다 이게 기하학적으로 무슨 뜻인지 확인해보면 A는 정방 행렬이고 λ는 고유값이고 (상수임!) x가 교유 벡터이다 Ax는 x라는 벡터를 A에 대해 선형 변환을 하는 것이다 λx는 x라는 벡터를 λ로 scaling (늘리거나 줄임) 것이다->왜냐 λ는 상수이기 때문이다 즉 A로 선형변환 했을 때 방향이나 차원등은 변하지 않고 λ의 크기로 scaling만 되는 벡터들이 고유 벡터인 것이다 그리고 그 고유 벡터가 A로 선형변환 됐을 때 커지거나 작아지는 정도 (scaling factor)가 λ인 고유 값이 된다 그래서 고유 벡터 마다 고유값이 있다 그러면 이들을 어떻게 구하는가? λ와 x 사이에 항등행렬(Identity Matrix)을 곱해준다 -> 일..

​ 행렬의 Trace는 그 행렬의 대각 성분들의 합이다 (좌측 상단 부터 우측 하단) ​ N x N 크기의 정방 행렬이 있다면 그 행렬의 trace는 아래와 같이 정의 된다 ​ ​ 그래서 trace는 행렬의 대각 성분들의 합으로 계산되어 스칼라 값이 됩니다. 행렬의 트레이스(trace)는 선형 대수학 및 기타 수학 분야에서 여러 흥미로운 성질과 응용을 가지고 있습니다. 예를 들어, 유사 변환(similarity transformations) 하에서 불변하며(변하지 않음), 행렬의 고유값(eigenvalues)의 합과 동일합니다. 물리학에서는 트레이스가 종종 에너지-운동량 텐서(energy-momentum tensor)의 식에서 나타납니다. ​ For a 2x2 matrix: ​ For a 3x3 matr..