eigenvalues & eigenvectors (고유값과 고유벡터)

 

728x90

일반적으로 고유값과 고유벡터를 배우면 위와 같은 식이 주어진다

이게 기하학적으로 무슨 뜻인지 확인해보면

 

A는 정방 행렬이고

λ는 고유값이고 (상수임!)

x가 교유 벡터이다

 

Ax는 x라는 벡터를 A에 대해 선형 변환을 하는 것이다

λx는 x라는 벡터를 λ로 scaling (늘리거나 줄임) 것이다->왜냐 λ는 상수이기 때문이다

 

즉 A로 선형변환 했을 때 방향이나 차원등은 변하지 않고

λ의 크기로 scaling만 되는 벡터들이 고유 벡터인 것이다

 

그리고 그 고유 벡터가 A로 선형변환 됐을 때 커지거나 작아지는 정도 (scaling factor)가 λ인 고유 값이 된다

 

그래서 고유 벡터 마다 고유값이 있다

 

그러면 이들을 어떻게 구하는가?

λ와 x 사이에 항등행렬(Identity Matrix)을 곱해준다 -> 일반적인 수식에 1의 곱샘이 생락된거와 비슷

위와 같이 모든항을 한쪽으로 이항시켜준다

 

이러한 상황에 =0이 되려면

죄측 행렬의 determinent가 0이 되어야 한다!

반응형

행렬식 (Determinent)에 대해서는 아래에 참고!

역행렬, Inverse Matrix, 라플라스 전개, Laplace Extension

역행렬은 Inverse Matrix라고 한다 전형적인 2x2 행렬은 이런 식으로 구한다 고등학교 때 암기해라고 외우는 공식이다 그리고 밑에 분모는 특별하게 이름을 붙혀 Determinent라고 한다 (행렬식) |A| = det(A) 모든 행렬이 역행렬이 있는 것은 아닌데 역행렬이 있는 행렬은 Invertable Matrix이고 determinent가 0이 아니며 = Non-Singular Matrix = Non-degenerate Matrix 반대로 Non-Invertable Matrix는 detrminent가 0이다 = SIngu...

tonnykang.tistory.com

 

ex) 직접 간단하게 2x2 행렬로 해보면

A라는 벡터가 있다고 하자

det(A-λI)가 0이 되어야하니

 

이 경우에는 Identity Matrix I도 2x2 행렬이다

그래서 계산해보면

 

이렇게 되면 이것을 Characteristic Equation이라고도 한다

λ에대한 간단한 방정식을 풀어보면

.

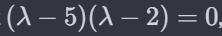
임을 알수 있다

 

고유 벡터 x를 구하려면 일단

λ_1=5 에 대해서는

2x2 정방행렬로 구했음으로

2차원 벡터일것임으로

이 방정식을 풀면

λ_1=5 에 대한 고유벡터는 아래와 같이 구해진다

똑같이 λ_2=3 에대해 방정식을 세워 풀어보면 아래와 같은 고유 벡터가 구해진다

"이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다."

 

또 알아두면 유용한 특징으로는

 

1. 고유값들의 곱이 행렬식과 같디

2. 고유 값들의 합이 행렬의 Trace와 같다

https://tonnykang.tistory.com/92

선형대수학, Trace

 

3. 행렬의 Transpose의 고유값과 고유벡터들도 같다