역행렬은 Inverse Matrix라고 한다
전형적인 2x2 행렬은
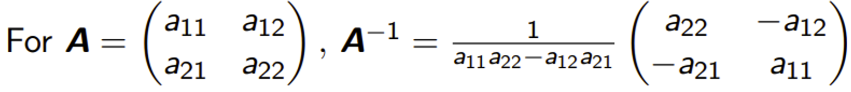
이런 식으로 구한다
고등학교 때 암기해라고 외우는 공식이다
그리고 밑에 분모는 특별하게 이름을 붙혀
Determinent라고 한다 (행렬식)

|A| = det(A)
모든 행렬이 역행렬이 있는 것은 아닌데
역행렬이 있는 행렬은
Invertable Matrix이고 determinent가 0이 아니며 = Non-Singular Matrix = Non-degenerate Matrix
반대로
Non-Invertable Matrix는 detrminent가 0이다 = SIngular Matrix = degenerate Matrix
또 추가적인 determinent의 성질로는

그러나 행렬은 2x2만 있나?
아닌 경우가 더 많을 것이다
그럼 한단계 나아가 3x3 행렬은 어떻게 구하는가?

역시나 공식화가 되어있다
더 길어졌지만 아직은 외울만하다
하지만 4x4? 아니면 그 이상의 크기의 행렬들은 어려워진다
이때 이용할 수 있는 것이
라플라스 전개 이다 (Laplace Extension)
알아보기전 알아야할 개념들이 몇개 있다
 이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다.
이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다.
Minors (소행렬)
Minor은 한 행렬의 원소의 위치를 i,j 라 했을때
그 원소가 해당하는 행과 열을 삭제한 행렬의 determinent이다

A라는 행렬 A_11의 Minor은 (A_11=4)
첫번째 행과 열을 삭제함으로

의 determinent인
2*2-0*0=4 가 된다
마찬가지로 A_23의 Minor은 다음과 같다 (A_23 = 0)
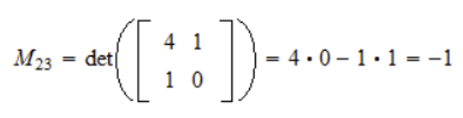
Cofactors (여인수)
Cofactor은 Minor에 부호 변화를 가해주면 된다
부호 변화는 이렇게 정의 된다

즉 그 원소의 좌표 i, j 의 합이 짝수면 1, 홀수면 -1이다
그래서
4x4 행렬의 부호 변화는 다음과 같이 나타낼 수 있다

그렇게 Cofactor은

이다 (M_ij 는 Minor(A_ij))
EX)
다음 행렬의 Determinent를 구하여라
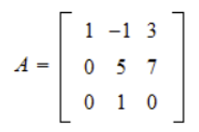
이 문제는 첫번째 열에 0이 가장 많음으로 계산하기 쉬워
A_11로 확장해서 전개하는것이 가장 효율적이다

공식을 대입 해도 되지만 차수가 커져도 전개 법만 알면
재귀적으로 풀면 되기에 공식을 외우는 것이 비효율적 이다
Cofactor Matrix (여인수 행렬)
행렬 A 의 여인수 행렬은 모든 원소들의 위치에 여인수가 그 원소 대신 있는 크기가 A와 같은 행렬이다

A의 determinent는 A의 원소와 그 원소의 Cofactor의 곱의 합이다
또
Cofactor Matrix의 Transpose는
Adjoint Matrix이다 (수반 행렬)

A의 Inverse는 이렇게 정의 되며
사실 처음 봤던
2x2 행렬의 행렬식도
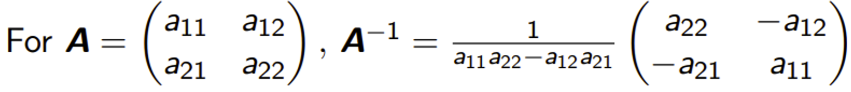
위에 식과 같다
<인공지능 AI 윤리>
https://tonnykang.tistory.com/67
[인공지능 윤리] Artificial Intelligence Ethics
데이터 과학을 하면서 지켜야 할 윤리와 주의해야 할 점들이 있습니다. 인과관계 ≠ 상관관계 이 두 용어는 종종 혼동되기도 하지만, 실제로는 다른 개념들입니다. 1. 인과 관계 (Causation): - 인과
tonnykang.tistory.com
'컴퓨터공학 > LG Aimers' 카테고리의 다른 글
| 대각 행렬 Diagonal Matrix (78) | 2024.02.08 |
|---|---|
| eigenvalues & eigenvectors (고유값과 고유벡터) (109) | 2024.02.02 |
| 선형대수학, Trace (81) | 2024.01.29 |
| [인공지능 윤리] Artificial Intelligence Ethics (77) | 2024.01.05 |
| [LG Aimers] LG 에서 주최하는 LG Aimers 4기 선정후기 (64) | 2024.01.02 |



