https://tonnykang.tistory.com/268
ADsP 데이터 분석 준 전문가 정리 10
https://tonnykang.tistory.com/267 ADsP 데이터 분석 준 전문가 정리 9https://tonnykang.tistory.com/266 ADsP 데이터 분석 준 전문가 정리 8https://tonnykang.tistory.com/265 데이터 준 분석가 R언어 기초https://tonnykang.tistory
tonnykang.tistory.com
회귀분석 Regression
회귀분석의 가정
선형성
- 독립변수와 종속변수가 선형적이어야한다
- 예외적으로는 2차 함수 회귀선을 갖는 다항회귀분석의 경우에는 괜찮다
독립성
- 단순회귀분석에서는 잔차와 독립변수의 값이 서로 독립이어야한다
- 독립변수가 여러 개인 다중회귀분석의 경우에는 독립변수들 간에 상관성이 없이 독립이어야한다
등분산성
- 분산이 같다는 의미 = 잔차들이 고르게 분포하고 있다는 의미이다
- 잔차의 중심에서 분산이 같아야 한다는 의미다
- 이를 만족하지 못하면 회귀선은 어떤 추세를 띄지 못하고 clustered된다
정규성
- 잔차항이 정규분포 형태를 띠는 것을 정규성을 만족한다고 한다
- Q-Q Plot에서 잔차가 오른쪽으로 상승하는 형태를 띄면 만족한다고 판단한다

최소제곱법으로 회귀계수 추정
- 최소제곱법을 통해 파라미터를 추정하고 추정된 파라미터들 통해 추세선을 그려 값을 예측하는 것이 회귀분석의 기본 알고리즘이다
- 실제 관측치와 추세선에 의해 예측된 점 사이의 거리, 즉 오차를 제곱해 더한 값을 최소화하는 것이다, 좌표평면상 다양한 추세선이 그려질 수는 있지만, 잔차의 제곱 합이 최소가 되는 추세선이 가장 합리적이다 → MSE 최소

SST = Sum of Squared Total
SSE = Sum of Squared Error
SSR = Sum of Squared Regression
회귀분석모형의 적합성
회귀분석의 분산분석표
독립변수가 1개라면 단순회귀분석, 2개 이상이라면 다중회귀분석을 시행한다
[단순선형회귀분석의 분산분석표]

[다중선형회귀분석의 분산분석표]

회귀모형의 통계성 유의성 검증
- 회귀모형의 귀무가설은 ‘모든 회귀계수는 0이다’이며 F-검정을 통해 확인한다
- F-검정은 분산의 차이를 확인할 때 사용되는데, 분산의 차이가 크다는 것은 회귀모형에서 회귀계수가 크다는 의미다
모형의 설명력
- 회귀모형의 설명력이 좋다는 의미는 데이터들의 분포가 회귀선에 밀접하게 분포하고 있다는 의미이다
- 회귀분석 결과를 분산분석하고, 도출된 결정계수 R^2로 모형의 설명력을 판단한다
- 결정계수 R^2이 1에 가깝다면 데이터들이 회귀선에 매우 밀접하게 분포한다는 것이며 곧 회귀모형의 예측력이 높다는 마로가도 같다

- 여기서 Q는 전체 데이터들의 편차들을 제곱하여 합한 값이며, Qe는 전체 데이터들의 잔차를 제곱하여 합한것이다

다중선형회귀분석
다중공선성
회귀분석에서 독립변수 간에 강한 상관관계가 나타나는 문제다
다중공선성이 존재하면 회귀분석의 기본 가정인 독립성에 위배된다
다중공선성의 진단
분상팽창요인 (VIF)을 구해 10을 넘는다면 보통 다중공선성이 있다고 판단할 수 있다
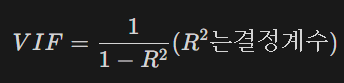
다중공선성 문제 해결법
- 문제가 발생하는 변수를 제거한다
- 주성분분석 (PCA)를 통해 차원을 축소한다, 아무 변수를 없에는게 아니고 원래 데이터가 가진 내재적 속성을 보존하면서 데이터를 축소하는 방법이다
- R에서 Scree Plot 스크리 산범도 를 이용해 주성분 개수를 선택한다
- 선형판별분석 LDA 로 차원을 축소한다, 이는 지도학습으로 데이터의 분포를 학습하여 결정경계를 만들어 데이터를 분류한다
- 특이값 분해 SVD로 차원을 축소한다, PCA와 다르게 행렬 모양에 상관 없이 적용할 수 있다
↔EVD
변수 선택에 사용되는 성능지표
벌점화 penalty 방식의 AIC와 BIC
- 회귀 모형은 변수의 수가 증가할 수록 편향(bias)는 작아지고 분산(variance)은 커지려는 경향이 있다
- 그래서 변수의 수가 많아 복잡해진 모형에 벌점, 즉 일종의 페널티를 주어 최적 회귀 방정식을 도출 하고자 하는 방법이다
AIC (Akaike Information Criteria) 아카이케 정보 기준
- MSE에 변수 수만큼 페널티를 주는 지표이다

BIC (Bayes Information Criteria) 베이즈 정보 기준
- AIC의 단점인 표본이 커질 때 부정확하다는 단점을 보완한 지표이다
- 큰 차이는 없지만 표본이 커질 경우 더 정호가한 결과가 나타난다
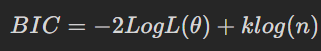
멜로우 CP (Mallow’s CP)
- 멜로우가 제안한 통계량으로 Cp값은 최소자승법으로 사용하여 추정된 회귀모형의 적합성을 평가하는데 사용된다
- CP값은 수정된 결정계수 (R^2) 및 AIC와 밀접한 관련이 있다
- CP값은 모든 벼수가 다 포함될 경우에 p값과 같아진다, 따라서 나쁜 모델은 CP값이 p값보다 클 때 이며 좋은 모델은 최소한 p값보다 작을 때다
단계적 변수 선택법
전진선택법 Forward Selection
가장 많은 영향을 줄 것으로 판단하는 변수부터 하나씩 추가해 모형을 선택한다
p-value가 가장 작은 변수
후진제거법 Backward Elimination
독립변수를 모두 포함하여 가장 적은 영향을 주는 변수부터 하나씩 제거하는 방법이다
p-value가 가장 큰 변수
단계별 방법 Stepwise Method
위 두방법을 보완한 방법이다
고급 선형회귀
과적합과 과소적합
Overfitting
https://tonnykang.tistory.com/136
Overfitting 과적합
오버피팅(overfitting)이란? 학습 데이터에 대해 과하게 학습하여 실제 데이터에 대한 오차가 증가하는 현상 train-set에서는 정확도 매우 높게 나옴, but test-set에서는 낮은 정확도 오버피팅이 발생하
tonnykang.tistory.com
Underfitting
정규화 선형회귀의 종류
라쏘 Lasso Regression
L1 규제라고도하며, L1 norm 값을 사용하여 가중치들의 절대값의 합을 최소화하는 것을 제약조건으로 추가한 방법이다
릿지 Ridge Rgression
L2 규제라고도 하며, L2 norm 값을 이요해 가중치들의 제곱합을 최소화하는 것을 제약조건으로 하는 방법이다
엘라스틱넷 Elastic Net
라쏘와 릿지를 결합한 모델이다
일반화 선형회귀의 종류
로지스틱 회귀 Logistic Regression
- 로지스틱 회귀는 종속변수가 범주형 변수 (0,1) 인 경우로 의학연구에 주로 많이 사용된다
포아송 회귀 Poisson Regression
- 종속변수가 특정 시간 동안 발생한 사건의 건수에 대한 도수 자료인 경우이면서, 종속변수가 정규분포를 따르지 않거나 등분산성을 만족하지 못하는 경우에 포아송 회귀 분석이 사용된다
- Maximum Likelihood Estimation, MLE를 이용해 모수를 추정한다
'컴퓨터공학 > ADsP' 카테고리의 다른 글
| ADsP 데이터 분석 준 전문가 정리 13 (51) | 2024.07.19 |
|---|---|
| ADsP 데이터 분석 준 전문가 정리 12 (51) | 2024.07.18 |
| ADsP 데이터 분석 준 전문가 정리 10 (58) | 2024.07.16 |
| ADsP 데이터 분석 준 전문가 정리 9 (50) | 2024.07.15 |
| 데이터 준 분석가 R언어 기초 (53) | 2024.07.14 |