https://tonnykang.tistory.com/270
ADsP 데이터 분석 준 전문가 정리 12
주성분분석 PCA여러 개의 변수 중 서로 상관성이 높은 변수들의 선형 결합으로 새로운 변수(주성분)을 만들어 기존변수를 요약 및 축소하는 분석 방법이다변수를 축소하여 모형의 설명력을 높임
tonnykang.tistory.com
시계열 분석
일정 시간 간격으로 기록된 자료들에 대하여 특성을 파악하고 미래를 예측하는 분석방법이다
시계열 자료의 자기상관성
이 말은 서로 이웃하는 자료들끼리 일종의 상관관계를 가진다는 말이다
→ 시간적으로 앞 뒤 데이터와 관련 있음
여기서 공분산의 개념을 살펴봐야한다 Covariance
→ 두 개의 확률 변수의 선형관계를 나타낸다
→ 하나의 증감에 따른 다른 확률 변수의 증감 경향에 대한 측도다
공분산이 0 이면 두 변수는 독립적인 확률변수로 봐야한다
↔ 그러나 대부분의 시계열 자료들은 자기상관성을 가지기 때문에 공분산은 0이 아니다
시계열 분석의 자료
- 크게 정상성 시계열과 비정상성 시계열 자료로 구분됨
- 대부분 자료는 바정상성 시계열 자료다
- 하지만 분석하려면 정상성 자료여야함
시계열 자료의 정상성 조건
일정한 평균
모든 시점에 대하여 평균이 일정해야한다
그렇지 않으면 차분을 통해 정상화 할 수있다
차분 → 현 시점의 자료값에서 전 시점의 자료값을 빼는 것이다


일정한 분산
모든 시점에 대하여 분산이 일정해야한다
그렇지 않다면 변환을 통해 정상화할 수 있다
→ 지수 혹은 로그를 취해 분산의 크기를 안정시킬 수 있다


시차에만 의존하는 공분산
공분산은 단지 시차에만 의존하고 특정 시점에 의존하지 않는다
t는 시점, s는 시차라고 했을 때
t시점과 t+s시점의 공분산과 t시점과 t-s 시점의 공분산은 서로 같다
→큰 경향은 같다

시계열 모형
자기회귀 (AR: Autoregressive) 모형
t라는 시점에서 값 yt는 이전시점들 n개에 의해 설명될 수 있음을 의미한다
특정 시점 t로부터 k번째 이전 시점들은 각각의 다른 가중치 값 thetak를 가지고 있다

여기서 at는 백색잡음으로 시계열 분석에서 평군이 0, 분산이 sigma^2를 따르는 오차항
→ 전에는 없고 현재에 있는 noise
이동평균(MA: Moving Average)모형
백색잡음들의 선형 결합으로 이루어져 있으며 항상 정상성을 만족한다
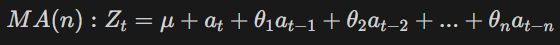
자기회귀누적이동평균모형
ARIMA: Autoregressive Integrated Moving Average
비정상 시계열 자료를 다룰 수 있는 모형으로 현실에 존재하는 대부분의 시계열 자료를 설명할 수 있다
→ 차분이나 변환을통해 정상화도 가능하다
'컴퓨터공학 > ADsP' 카테고리의 다른 글
| ADsP 데이터 분석 준 전문가 정리 15 (56) | 2024.07.21 |
|---|---|
| ADsP 데이터 분석 준 전문가 정리 14 (37) | 2024.07.20 |
| ADsP 데이터 분석 준 전문가 정리 12 (52) | 2024.07.18 |
| ADsP 데이터 분석 준 전문가 정리 11 (59) | 2024.07.17 |
| ADsP 데이터 분석 준 전문가 정리 10 (58) | 2024.07.16 |