반응형
k-NN(k-Nearest Neighbors)는 지연 학습 알고리즘이다.
정의
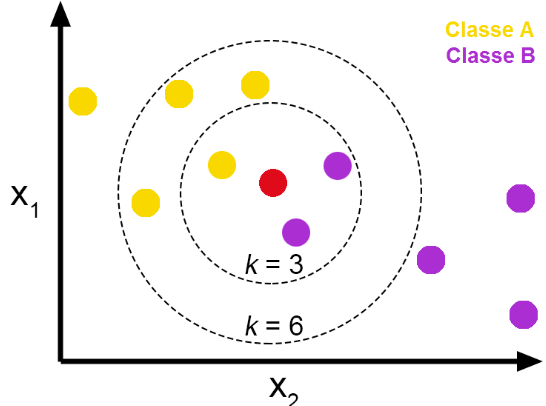
k-NN은 함수가 Locally (가깝게) 근사되고, 모든 계산이 함수 평가 시점까지 미뤄지는 지연 학습 알고리즘이다. 분류와 회귀 모두에서 알고리즘은 Feature 공간에서 가장 가까운 k개의 훈련 예제를 기반으로 출력을 예측한다.
작동 방식
- 학습 단계:
- k-NN의 학습 단계는 없다! Lazy Learning Algorithm
- 학습 데이터는 단순히 저장되고, 명시적인 모델은 학습되지 않는다.
- 예측 단계:
- 분류:
- 주어진 테스트 인스턴스에 대해, 알고리즘은 테스트 인스턴스와 모든 훈련 인스턴스 간의 거리를 계산한다.
- 가장 가까운 k개의 훈련 인스턴스(이웃, neighbor)를 식별한다.
- 테스트 인스턴스의 클래스 레이블은 k개 이웃 중 다수결 투표로 결정된다. 테스트 인스턴스는 k 최근접 이웃 중 가장 많은 클래스로 할당된다. Hard Voting!
- 회귀:
- 분류와 유사하지만, 투표 대신 알고리즘은 k 최근접 이웃의 타겟 값 평균(때로는 가중 평균)을 계산하여 출력을 예측한다. Soft Voting!
- 분류:
728x90
주요 구성 요소
반응형
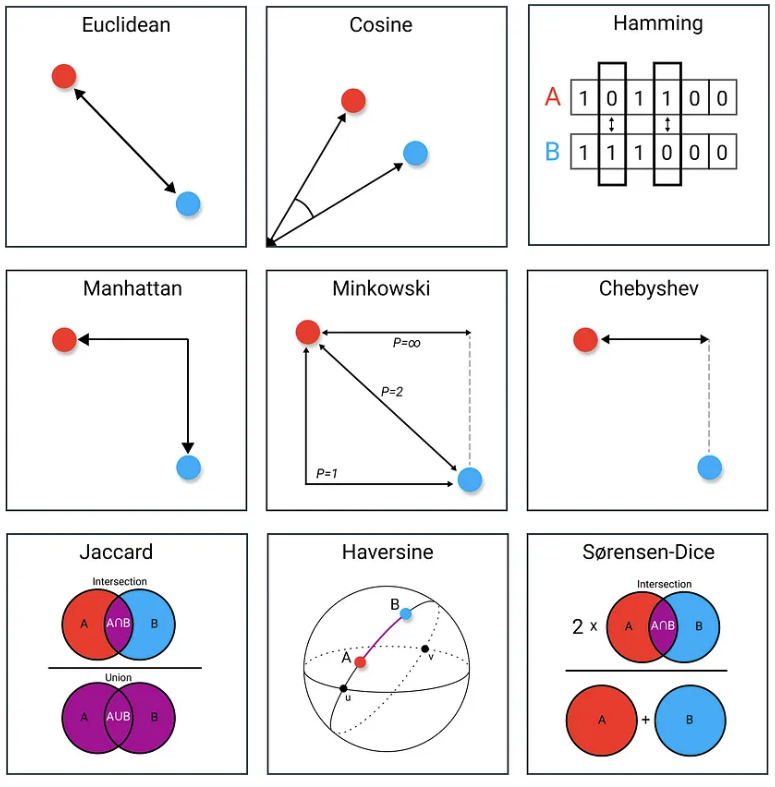
- 거리 측정 방식:
- 거리 측정 방식의 선택은 k-NN에서 매우 중요하다. 일반적인 거리 측정 방식들은 아래와 같다:
- Euclid 유클리드 거리: 𝑑(𝑥,𝑦)=∑𝑖=1𝑛(𝑥𝑖−𝑦𝑖)2
- Manhattan 맨하탄 거리: 𝑑(𝑥,𝑦)=∑𝑖=1𝑛∣𝑥𝑖−𝑦𝑖∣
- Minkowski 민코프스키 거리: 유클리드 거리와 맨하탄 거리를 포함하는 일반화된 거리 측정 방식
- 코사인 유사도: 텍스트 데이터에 자주 사용되며, 두 벡터 간 코사인 값을 측정해 비교한다.
- 거리 측정 방식의 선택은 k-NN에서 매우 중요하다. 일반적인 거리 측정 방식들은 아래와 같다:
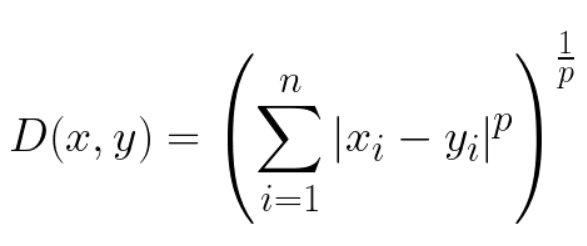
p=inf -> Chebyshev Distance
p=1-> Euclidian Distance
p=2-> Manhattan Distance
- k 값 선택:
- k 값은 고려할 최근접 이웃 수를 결정하는 하이퍼파라미터입니다. k 값의 선택은 알고리즘 성능에 큰 영향을 미친다:
- 작은 k 값(예: k=1)은 Overfitting 과 노이즈가 있는 예측을 초래할 수 있습니다.
- 큰 k 값은 더 부드러운 결정 경계를 만들지만 Underfitting 될 수 있습니다.
- 종종 k 값은 교차 검증을 통해 최적의 균형을 찾기 위해 선택된다.
- k 값은 고려할 최근접 이웃 수를 결정하는 하이퍼파라미터입니다. k 값의 선택은 알고리즘 성능에 큰 영향을 미친다:
- 이웃 가중치 부여:
- 때로는 단순 다수결 투표나 평균 대신, 이웃에 거리에 따른 가중치를 부여할 수 있습니다. 더 가까운 이웃에 더 큰 가중치가 주어진다.
장단점
장점
- 단순성: 이해하고 구현하기 쉽다.
- 학습 단계 없음: 학습 시간이 중요한 시나리오에서 유용하다.
- 다용도성: 분류와 회귀 모두에 사용할 수 있다.
단점:
- 계산 복잡성: 모든 훈련 인스턴스에 대한 거리를 계산해야 하므로 대규모 데이터셋에 대한 예측 단계가 느릴 수 있다.
- 저장 요구 사항: 모든 훈련 데이터를 저장해야 한다.
- 차원의 저주: 고차원 데이터에서 거리의 의미가 약해지면서 성능이 저하될 수 있다.
- 무관한 특성에 민감함: 특성이 적절히 스케일링되지 않거나 무관한 특성이 있으면 성능에 영향을 미칠 수 있다.
요약
k-최근접 이웃 알고리즘은 단순성과 효과성으로 잘 알려진 머신러닝 도구 중 하나다.
예측을 위해 가장 가까운 훈련 예제를 활용함으로써 k-NN은 다양한 도메인에서 분류와 회귀 작업 모두에 사용될 수 있습니다.
그러나 거리 측정 방식, k 값 선택, 특성 스케일링에 대한 신중한 고려가 필수적입니다.
반응형
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| 딥러닝과 뉴런, 파이썬 케라스 코드 (83) | 2024.07.29 |
|---|---|
| 파이선 pandas 라이브러리 get_dummies() (64) | 2024.05.28 |
| Naive Bayes model, 네이브 베이즈 모델 (75) | 2024.05.27 |
| Scikit-learn, Imputer 결측값 처리기 (null values, nan) (57) | 2024.04.05 |
| K-fold Cross Validation 심화편 (Data Leakage, Stratified) (56) | 2024.04.04 |