네이브 베이즈는 베이즈 정리에 기반한 간단하지만 효과적인 확률론적 분류기의 집합이다.
"네이브(Naive)"라는 이름은 각 특성(또는 예측 변수)들이 클래스 레이블에 대해 서로 독립적이라고(independent) 가정하기 때문에 붙여졌다.
실제로 미국에서는
나이브
라고 발음한다
단순한 사람보고
Don't be so Naive!
이런식으로 사용된다
Independent 하다는 이 가정은 실제 데이터에서는 자 만족되지 않지만 계산을 크게 단순화시켜 준다.
Bayes' Theorem 베이즈 이론
P(C|X) = P(X|C)P(C) / P(X)
여기서:
- P(C|X)는 특성 X가 주어졌을 때 클래스 C의 사후 확률이다.
- P(X|C)는 클래스 C가 주어졌을 때 특성 X를 관측할 가능성인 값으로, 훈련 데이터 (Train Set) 로부터 얻을 수 있다.
- P(C)는 클래스 C의 사전 확률입니다. Prior Probability
- P(X)는 특성 X를 관측할 주변 확률로, 또한 훈련 데이터에서 구할 수 있다. Marginal Probability
Prior vs Marginal Probability

주변 확률(Marginal Probability)은 무조건부 Unconditional 확률이라고도 하며, 다른 사건을 고려하지 않고 어떤 사건이 발생할 확률을 의미한다.
이는 단일 사건의 확률로, 다른 변수의 모든 가능한 결과에 대해 합산한 것이다.
- 예시:X가 주사위를 굴렸을 때의 결과를 나타낸다면, 주변 확률 P(X=4)는 공정한 6면체 주사위가 4가 나올 확률인 1/6다.
사전 확률(Prior Probability) 또는 단순히 사전(Prior)은 새로운 증거나 정보를 고려하기 전의 어떤 사건이 발생할 확률을 말합니다. 이는 이전의 지식이나 가정에 기반하여 그 사건에 대한 초기 신념의 정도를 반영합니다.
- 예시: C가 무작위로 선택된 이메일이 스팸인 사건을 나타낸다면, 사전 확률 P(C=스팸)은 훈련 데이터셋에서 스팸 이메일의 비율이다.
Naive Bayes Classifier 베이즈 분류기
분류 문제에서 목표는 사후 확률 P(C|X)를 극대화하는 클래스 레이블 C를 결정하는 것이다.
네이브 가정은 각 특성이 클래스 레이블에 대해 조건부 독립이라고 가정함으로써 우도 P(X|C)의 계산을 단순화합니다: P(X|C) = P(x_1, x_2, ..., x_n|C) = P(x_1|C)P(x_2|C) ... P(x_n|C)
여기서 x_1, x_2, ..., x_n은 개별 특성입니다.

- 훈련 단계 Training:
- 각 클래스에 대한 사전 확률 P(C)를 계산한다. Target Value!
- 각 클래스와 각 특성에 대해 P(x_i|C)를 계산한다.
- 가우시안 네이브 베이즈의 경우 각 클래스에 대한 feature의 평균 (mean)과 분산 (variance)을 계산한다.
- 다항 분포 및 베르누이 네이브 베이즈의 경우 각 클래스에 대한 각 특성의 발생 횟수를 계산한다.
- 예측 단계 Prediction:
- 새로운 관측치 X에 대해 베이즈 정리를 사용하여 각 클래스의 확률을 계산한다.
- 확률이 가장 높은 클래스를 선택합니다. Classified!
네이브 베이즈 분류기에는 특성 데이터의 분포를 다르게 가정하는 여러 변종이 있다:
- 가우시안 네이브 베이즈: 특성이 정규 분포를 따른다고 가정하며, 연속적인 데이터에 적합합니다.
- 다항 분포 네이브 베이즈: 특성이 개수나 빈도를 나타낸다고 가정하며, 단어 개수나 단어 빈도가 특성인 텍스트 분류 문제에 적합합니다.
- 베르누이 네이브 베이즈: 특성이 이진(0 또는 1)이라고 가정하며, 이진/부울 특성 벡터에 적합합니다.
Gaussian Naive Bayes 가우시언 네이브 베이즈
추측:
- feature들이 정규분포를 따른다고 가정한다. Normal(Gaussian) Distribution!
.

- 그럼으로 연속적인 값에 적절하다
학습 Training:
- Target 값 C 마다 그리고 각 Feature Xi마다 , 평균과 (μCi) 분산 (σCi2) 을 계산한다
- 이 파라미터들은 확률 P(Xi∣C) 를 Gaussian probability density function 을 통해 계산되는데 활용된다
모델링 Modeling:
- lass C 일때 feature value xi 일 확률은 Gaussian distribution을 사용해 계산된다:

그 후 Bayes' Theorem 을 통해 확률이 계산된다!
Multinomial Naive Bayes 다항 네이브 베이즈

추측:
- feature들이 counts or frequencies (횟수) 를 의미함을 가정한다
- text classification problems (문자 분류 문제)에 적절하다, 단어의 빈도, 용어 출현 횟수 등..
학습 Training:
- class C 와 feature (word) Xi마다 , class C에서의 빈도를 계산한다. Counting!
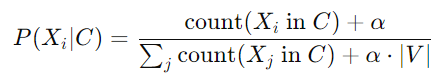
𝛼 는 smoothing Parameter이고
|V|는 단어들의 갯수이다, Unique Vocabulary
그 후 Bayes' Theorem 을 통해 확률이 계산된다!
Bernoulli Naive Bayes 베르누이 네이브 베이즈
추측:
- features are binary (0 or 1). 이진값으로 추측됨!
- binary/boolean feature vectors에 적합함! True or False!
Training:
- class C 와 각 feature Xi 마다, class C일 떄 feature Xi 가 1 일 확률을 구해준다 :
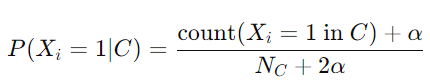
N_c는 C class의 instance의 갯수이
그 후 Bayes' Theorem 을 통해 확률이 계산된다!
훈련 및 모델링에서의 주요 차이점
1. Feature 가정:
- 가우시안 네이브 베이즈: 연속 특성이 가우시안(정규) 분포를 따른다고 가정.
- 다항 분포 네이브 베이즈: 이산 특성이 개수나 빈도를 나타낸다고 가정.
- 베르누이 네이브 베이즈: 이진 특성이 존재 유무를 나타낸다고 가정.
2. Likelihood 계산:
- 가우시안 네이브 베이즈: 특성의 평균과 분산을 사용하여 가우시안 우도를 계산합니다.
- 다항 분포 네이브 베이즈: 단어 개수와 상대 빈도를 사용하여 우도를 계산합니다.
- 베르누이 네이브 베이즈: 이진 지시자와 존재/부재 확률을 사용하여 우도를 계산합니다.
3. 적합성:
-가우시안 네이브 베이즈: 연속 데이터(예: 물리량 측정)에 적합합니다.
-다항 분포 네이브 베이즈: 단어 개수나 빈도가 특성인 텍스트 데이터에 적합합니다.
-베르누이 네이브 베이즈: 단어 존재 유무가 이진 특성인 텍스트 데이터에 적합합니다.
Naive Bayes의 장단점
장점: Lazy Training!
- 간단하고 구현이 쉽다.
- 적은 양의 훈련 데이터만 필요하다.
- 이진 및 다중 클래스 분류 문제 모두를 처리할 수 있다.
- 시간과 메모리 측면에서 효율적이다.
단점: Independency!
- 특성 독립성 가정이 현실적이지 않은 경우가 많다.
- 이 가정이 크게 위배되면 성능이 저조할 수 있다.
- 특성 간 상관관계가 높으면 효과적이지 않다.
요약하면, 네이브 베이즈는 조건부 독립성 가정의 단순성을 활용하여 다양한 도메인, 특히 텍스트 분류와 같이 특성 분포가 명확한 시나리오에서 효율적이고 효과적인 분류를 가능하게 하는 직관적이면서도 강력한 분류기이다.
Base Model 로 매우 적합!
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| 딥러닝과 뉴런, 파이썬 케라스 코드 (83) | 2024.07.29 |
|---|---|
| 파이선 pandas 라이브러리 get_dummies() (64) | 2024.05.28 |
| k-Nearest Neighbors (k-NN) 모델 KNN (69) | 2024.05.26 |
| Scikit-learn, Imputer 결측값 처리기 (null values, nan) (57) | 2024.04.05 |
| K-fold Cross Validation 심화편 (Data Leakage, Stratified) (56) | 2024.04.04 |