우리들의 T'SPACE

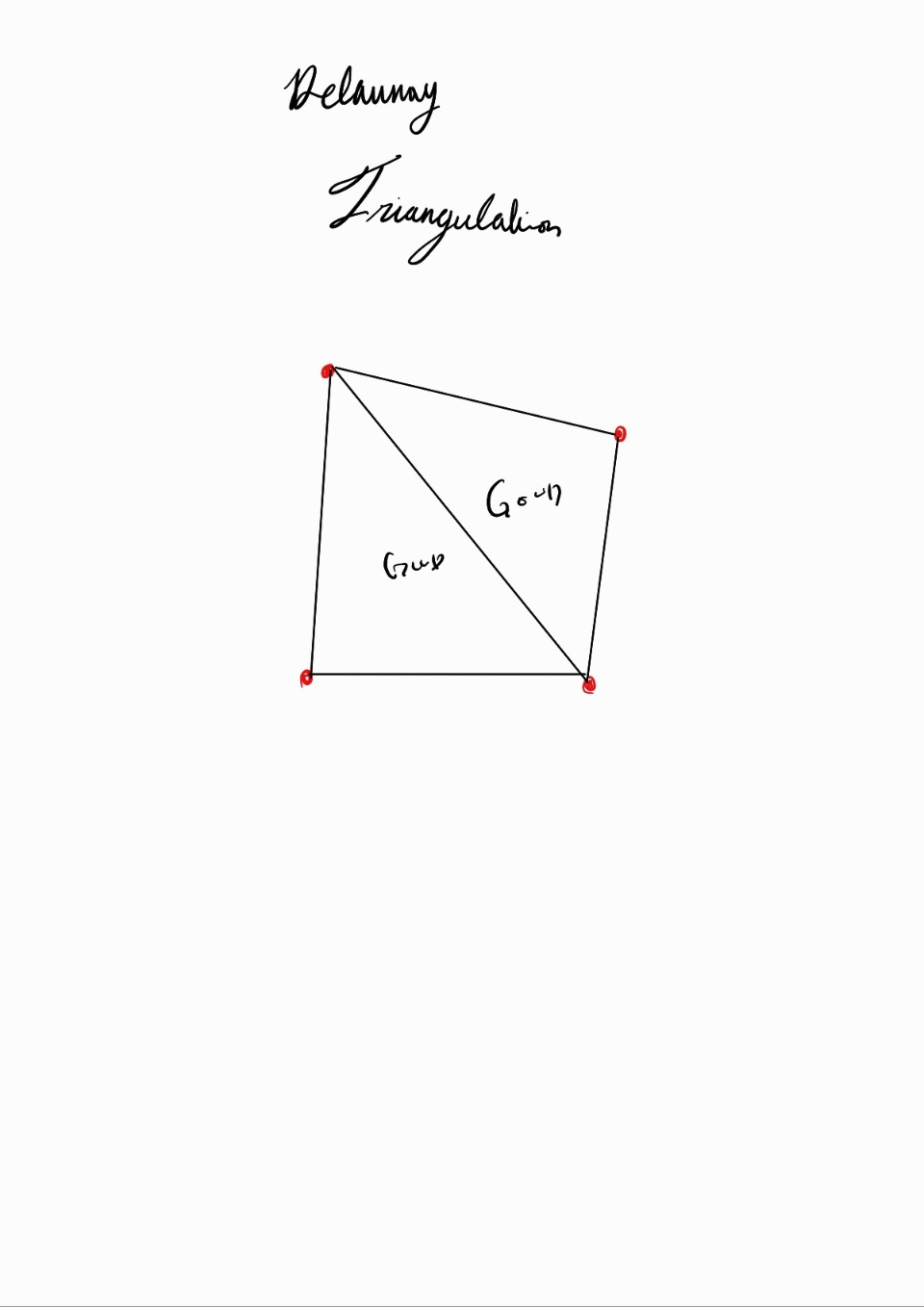
Delaunay Triangluation점들을 연결하는 최적의 방법 공간 데이터를 다루는 많은 분야에서 들로네 삼각분할(Delaunay Triangulation)은 핵심적인 기법으로 사용됩니다. 이 방법은 평면 위의 점들을 삼각형으로 연결하여 공간을 분할하는데, 단순히 연결하는 것이 아니라 특별한 기준을 따릅니다. 바로 삼각형들의 내각의 최소값이 최대가 되도록 하는 것입니다. 왜 이런 기준을 따르는 걸까요? 들로네 삼각분할의 핵심은 '빈 외접원 특성' Empty Circumcircle Property에 있습니다.이 특성을 충족시키기 위해 내각이 작은 삼각형 대신 내각이 큰 삼각형을 선택하게 되고, 이로 인해 "형태가 좋은" 삼각형들이 만들어집니다.예를 들어, 비 들로네 삼각분할에서 볼 수 있는 꼭짓점 V..

Convex Hull은 점들의 집합이 있을때 이 모든 점들을 포함하는 크기가 최소인 Convex Polygon을 찾는 문제이다Convexity 쉽게 말해 위처럼 집합 내에 있는 두 점을 연결한 선분이 집합 내에 있어야Convex하다고 할 수 있다하지만 우리가 찾는 것은 Convex Polygon 다각형임으로 모든 내각이 180도 이하라는 조건이 또 붙는다(180도는 각이 아님 ㅋ) 가장간단한 풀이 방법은 뭘까?? 좀 간지나게 mechanical way 라고 말하는데 2차원 평면에 수직되게 못을 점들과 대응되게 박아넣은뒤 고무줄을 늘려 풀어주면알아서 착! 감기며 Convex Hull 문제의 해를 구하게 된다 이렇게 시각적으로는 너무나 쉬운 내용이지많은 컴퓨터로 구현 혹은 알고리즘으로 정의 내리기가 매우 어..