Delaunay Triangluation
점들을 연결하는 최적의 방법
공간 데이터를 다루는 많은 분야에서 들로네 삼각분할(Delaunay Triangulation)은 핵심적인 기법으로 사용됩니다. 이 방법은 평면 위의 점들을 삼각형으로 연결하여 공간을 분할하는데, 단순히 연결하는 것이 아니라 특별한 기준을 따릅니다. 바로 삼각형들의 내각의 최소값이 최대가 되도록 하는 것입니다.
왜 이런 기준을 따르는 걸까요? 들로네 삼각분할의 핵심은 '빈 외접원 특성' Empty Circumcircle Property
에 있습니다.
이 특성을 충족시키기 위해 내각이 작은 삼각형 대신 내각이 큰 삼각형을 선택하게 되고, 이로 인해 "형태가 좋은" 삼각형들이 만들어집니다.
예를 들어, 비 들로네 삼각분할에서 볼 수 있는 꼭짓점 V2와 V4에서의 예각을 가진 삼각형 대신, V1과 V3을 연결하는 모서리로 대체하면 최소 각도가 최대화되어 들로네 삼각분할이 완성됩니다.

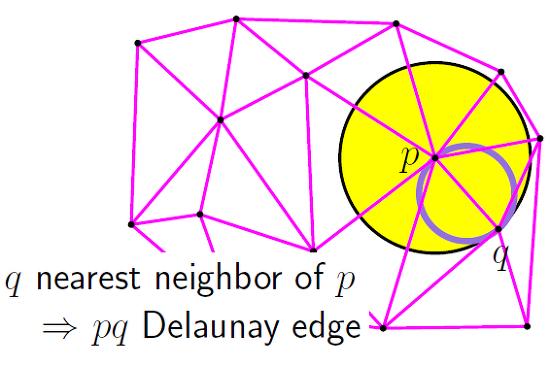
들로네 삼각분할의 또 다른 중요한 특징은 최근접이웃 방식으로 점을 연결한다는 것입니다.
이 두 가지 특성 - 형태가 좋은 삼각형과 최근접이웃 관계 - 은 실제 응용에서 매우 중요한 의미를 갖습니다. 특히 산점 데이터 보간에서 들로네 삼각분할이 널리 사용되는 이유가 바로 여기에 있습니다.
들로네 삼각분할의 가장 핵심적인 특징인 "빈 외접원 특성"에 대해 자세히 살펴보겠습니다.
이는 "어떤 삼각형의 외접원도 그 삼각형의 세 꼭지점을 제외한 다른 어떤 점도 포함하지 않는다"는 것을 의미합니다. 2차원 점 집합에서 이 특성은 매우 중요합니다. 예를 들어, 삼각형 T1과 T2의 외접원을 그렸을 때, 각 외접원 내부에 다른 점이 포함되어 있지 않다면 이는 들로네 삼각분할의 조건을 만족하는 것입니다.
The Circumcircle
외접원: 들로네 삼각분할의 핵심 요소
기하학에서 우리는 세 개의 비공선점(즉, 한 직선 위에 있지 않은 점들)이 유일한 원을 정의한다는 것을 알고 있습니다. 이를 바탕으로, 불규칙 삼각망(TIN)의 각 삼각형은 '외접원'이라는 특별한 도형과 연관됩니다. 이 외접원의 특성을 이해하는 것은 들로네 삼각분할을 깊이 있게 이해하는 데 매우 중요합니다.

위에 그림만 살펴보아도
둔각을 가지고 있는 외접원은 그렇지 않은 원보다 훨씬 큰 것을 볼 수 있다
"좋지 않은" 들로네 삼각형이다
외접원의 주요 특성들을 살펴보면:
1. 이름에서 알 수 있듯이, 외접원은 연관된 삼각형을 완전히 감싸고 있습니다.
2. 가늘고 긴 삼각형은 비슷한 크기의 균형 잡힌 삼각형보다 더 큰 외접원을 만듭니다.
3. 가늘고 긴 삼각형에서는 삼각형이 차지하지 않는 원의 면적 비율이 균형 잡힌 삼각형보다 상대적으로 더 큽니다.
4. 외접원의 중심이 반드시 삼각형 내부에 있을 필요는 없습니다. 따라서 큰 외접원이 차지하는 영역은 연관된 삼각형이 정의하는 영역을 훨씬 넘어설 수 있습니다.
이러한 특성들을 이해하면, 외접원이 들로네 기준을 정의하는 데 핵심적인 역할을 한다는 것을 알 수 있습니다. 구체적으로, 삼각분할이 "들로네 최적"이 되기 위해서는 다음 조건들을 만족해야 합니다:
1. 메쉬에 의해 형성된 모든 삼각형은 퇴화 (Degenerate) 되지 않아야 합니다. 즉, 세 개의 공선점이 하나의 삼각형으로 연결되어서는 안 됩니다. 그런 삼각형은 면적이 0이 되고, 결과적으로 무한대 반경의 외접원을 가지게 됩니다.
2. 메쉬의 모든 삼각형은 해당 삼각형을 정의하는 세 꼭짓점을 제외하고는 메쉬의 다른 어떤 꼭짓점도 포함하지 않는 외접원을 생성해야 합니다.
이러한 조건들은 들로네 삼각분할이 왜 "좋은" 삼각형들을 만들어내는지를 설명합니다. 외접원이 다른 점들을 포함하지 않도록 함으로써, 가능한 한 균형 잡힌 삼각형들이 형성되고, 이는 결과적으로 더 정확한 보간과 더 효율적인 계산을 가능하게 합니다.
Degenerecy
들로네 삼각분할은 대부분의 경우 강력하고 유용한 기법이지만, 특정 상황에서는 그 고유성이 보장되지 않습니다.
이를 '퇴화(Degeneracy)' 현상, Degenerate 이라고 부르며, 이는 들로네 삼각분할을 적용할 때 주의해야 할 중요한 개념입니다.
퇴화 현상은 언제 발생할까요?
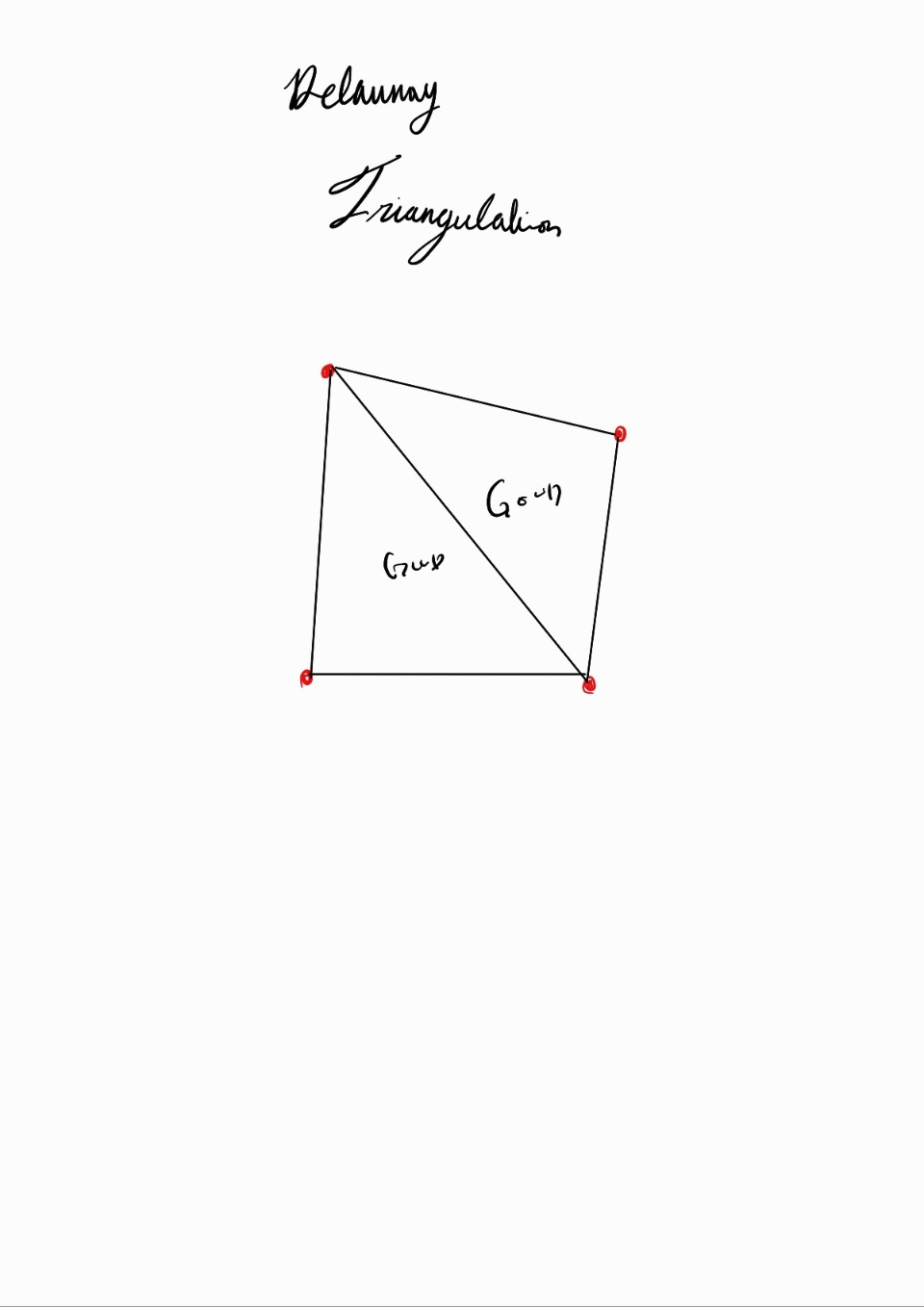
2차원 평면에서 4개 이상의 서로 다른 점들이 동일한 원 위에 놓여있을 때 발생합니다. 이런 상황에서는 들로네 삼각분할의 결과가 유일하지 않게 되어, 여러 가지 가능한 삼각분할이 존재하게 됩니다.

가장 간단한 예로 정사각형을 들 수 있습니다. 정사각형의 네 꼭짓점은 모두 같은 원 위에 있기 때문에, 이 점들에 대한 들로네 삼각분할은 고유하지 않습니다. 즉, 정사각형을 대각선으로 나누는 두 가지 방법 중 어느 것을 선택하더라도 들로네 삼각분할의 조건을 만족하게 됩니다.
이러한 퇴화 현상은 실제 응용에서 문제를 일으킬 수 있습니다.
예를 들어, 컴퓨터 그래픽스나 지리정보시스템에서 정확한 삼각분할이 필요한 경우, 퇴화 현상으로 인해 예기치 않은 결과가 나올 수 있습니다. 또한, 수치 계산의 정밀도 문제로 인해 실제로는 퇴화 상태가 아님에도 퇴화로 인식되는 경우도 있을 수 있습니다.
따라서 들로네 삼각분할을 구현하거나 사용할 때는 이러한 퇴화 현상을 고려해야 합니다. 일반적으로 이를 해결하기 위해 다음과 같은 방법들이 사용됩니다:
- 섭동법(Perturbation): 점들의 위치를 아주 조금씩 무작위로 이동시켜 퇴화 상태를 피합니다.
- 심볼릭 섭동(Symbolic perturbation): 수학적으로 점들의 위치를 미세하게 조정하는 방법입니다.
- 특별한 케이스 처리: 퇴화 상황을 감지하고 이를 특별히 처리하는 로직을 구현합니다.
https://arxiv.org/abs/1510.04608
Delaunay Triangulations of Degenerate Point Sets
The Delaunay triangulation (DT) is one of the most common and useful triangulations of point sets $P$ in the plane. DT is not unique when $P$ is degenerate, specifically when it contains quadruples of co-circular points. One way to achieve uniqueness is by
arxiv.org
결론적으로, 들로네 삼각분할의 퇴화 현상은 이 기법의 한계점을 보여주는 동시에, 더 정교한 알고리즘 개발의 필요성을 제시합니다. 실제 응용에서는 이러한 한계를 인식하고 적절히 대처하는 것이 중요합니다.
이러한 특성들로 인해 들로네 삼각분할은 컴퓨터 그래픽스, 지리정보시스템(GIS), 네트워크 설계 등 다양한 분야에서 널리 활용되고 있습니다. 점들 사이의 관계를 가장 효과적으로 표현할 수 있는 방법 중 하나이기 때문입니다.
Boyer-Watson Algorithm
1. 아래와 같은 arbiatary 한 set of points를 가정해보자,
본인은 더 쉬운 이해를 위해 점 4개로 설명해보겠다

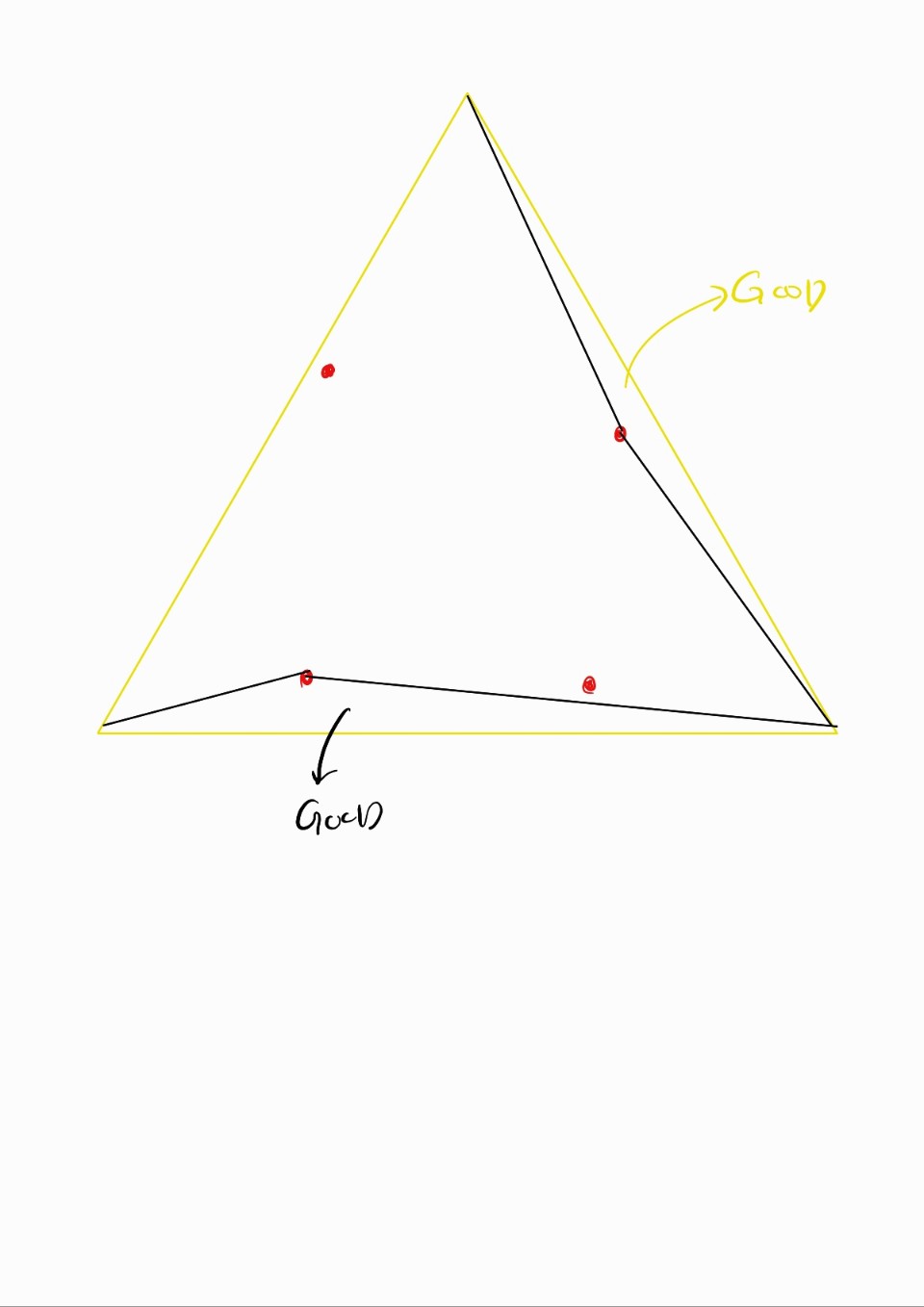
2. 모든 점들을 포함하는 SuperTriangle 을 그려준다, 크기는 무한히 커도 되며 점들을 모두 포함하기만 하면된다
우리는 초기 point들을 삼각형의 외접원이 포함한다면 Bad, 그렇지 않다면 Good으로 분류할 것이다
이 SuperTriangle은 4개 다 포함하기에 최악인 Bad이다
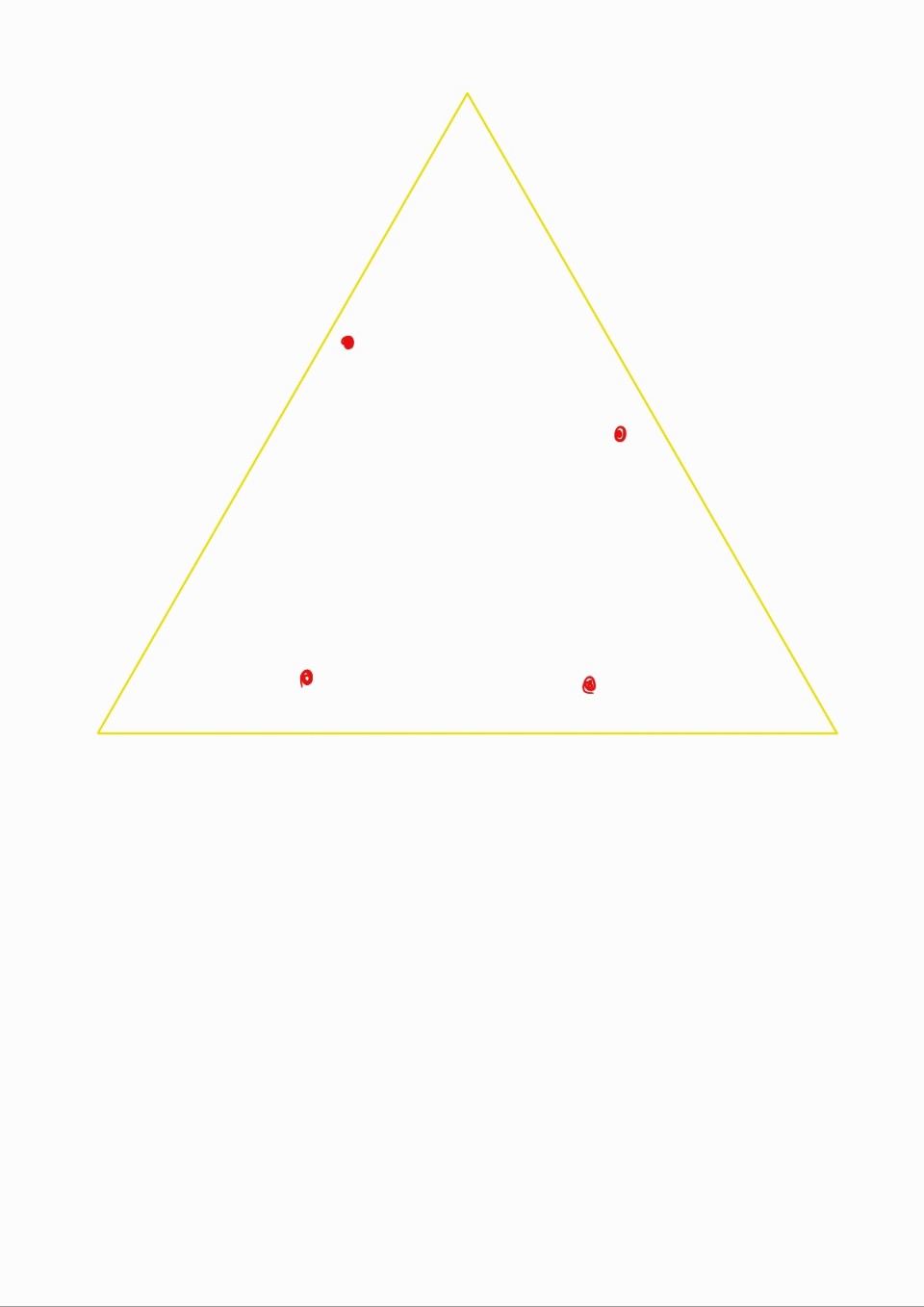
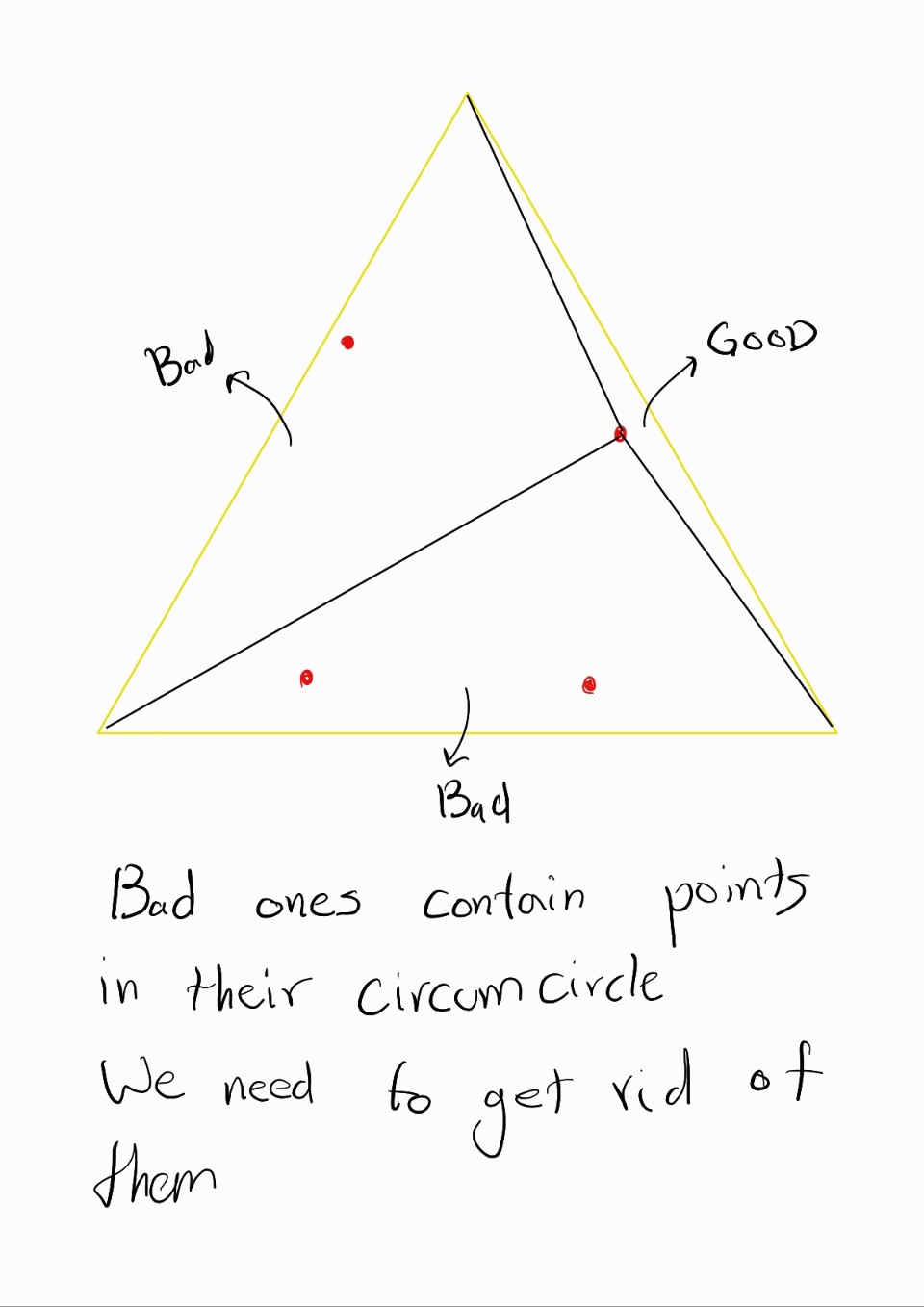
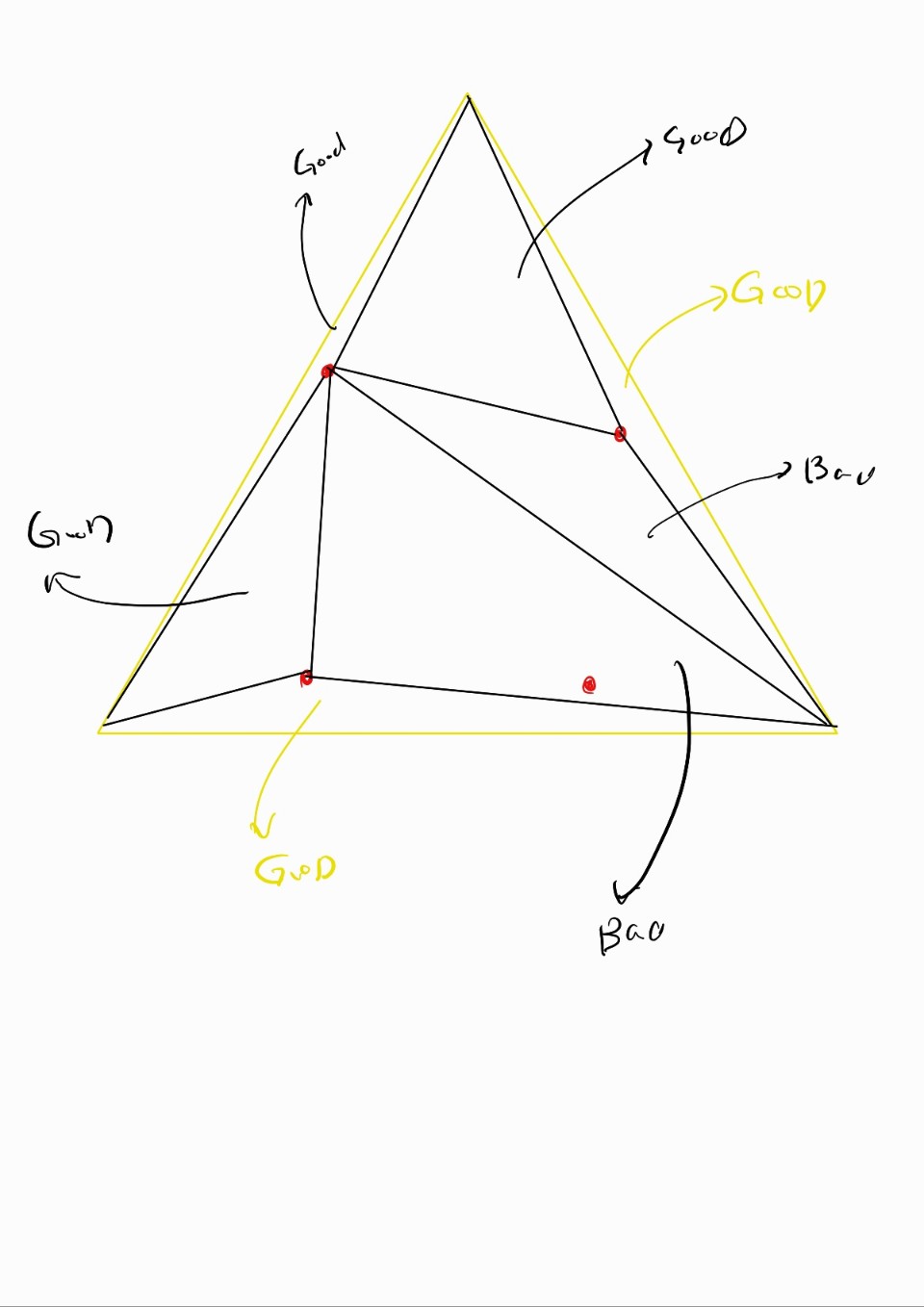
3. Bad (Invalid)한 삼각형은 우리는 Valid 한 삼각형의 집합으로 교체하는 게 목적이다
그래서 SuperTriangle을 아래와 같이 한 point를 정해 삼각형의 집합으로 대체해준다
하지만 대체된 이 삼각형들도 모두 Valid하지 않을 수 있으니
평가해준다
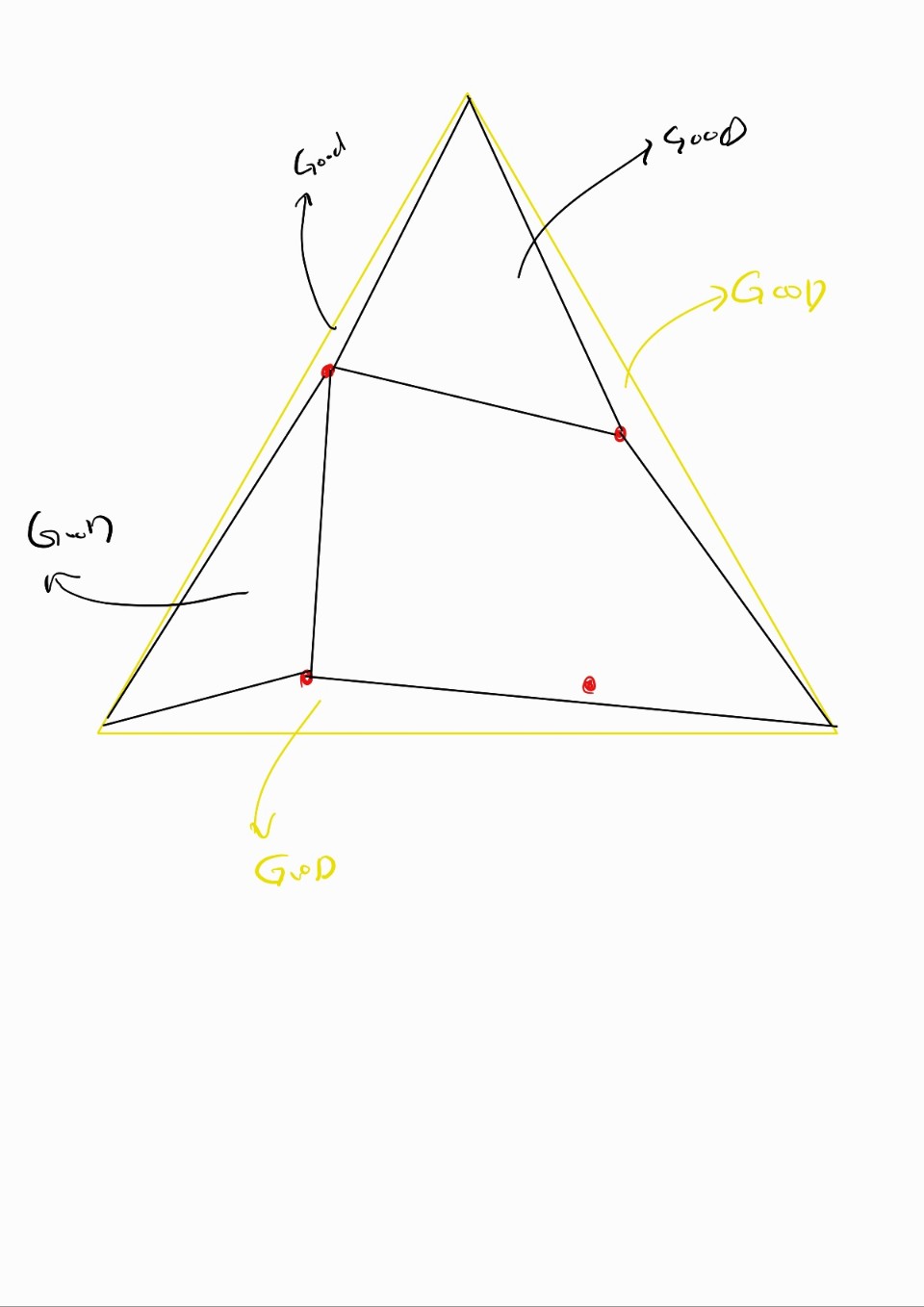
4. Invalid 한 삼각형들은 또 위와같은 방법으로 교체해준다
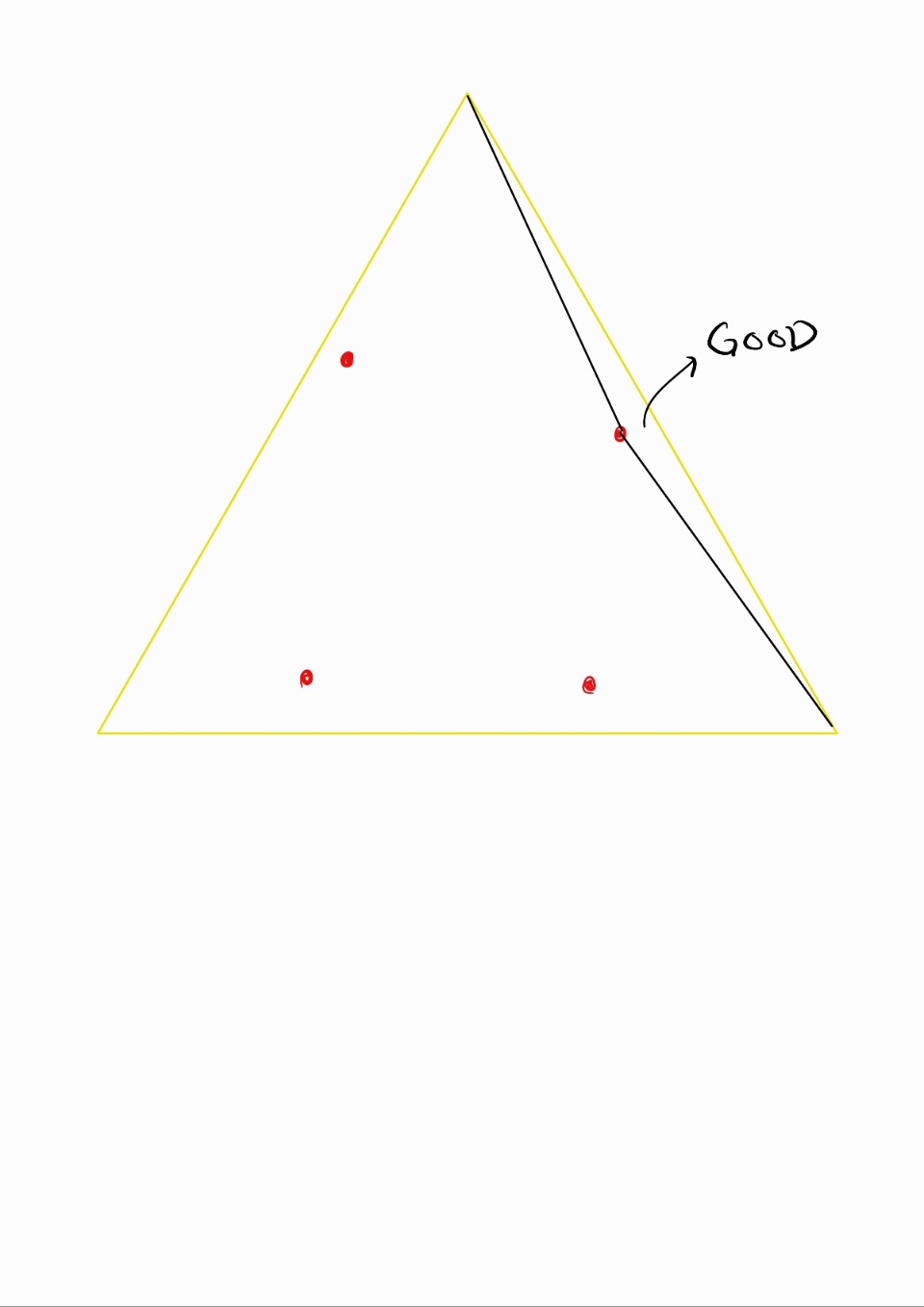
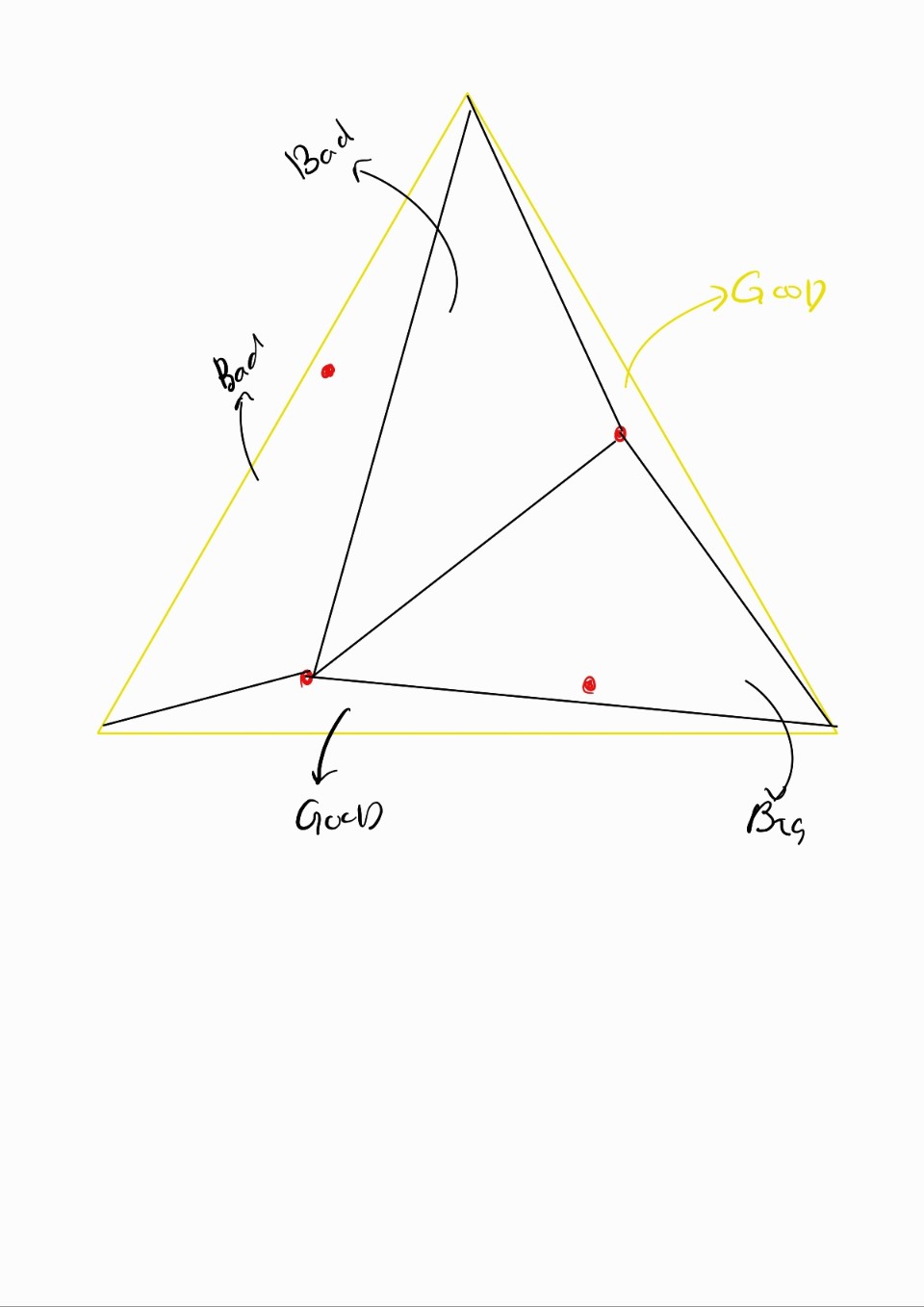
5. 모두 Valid할때 까지 반복
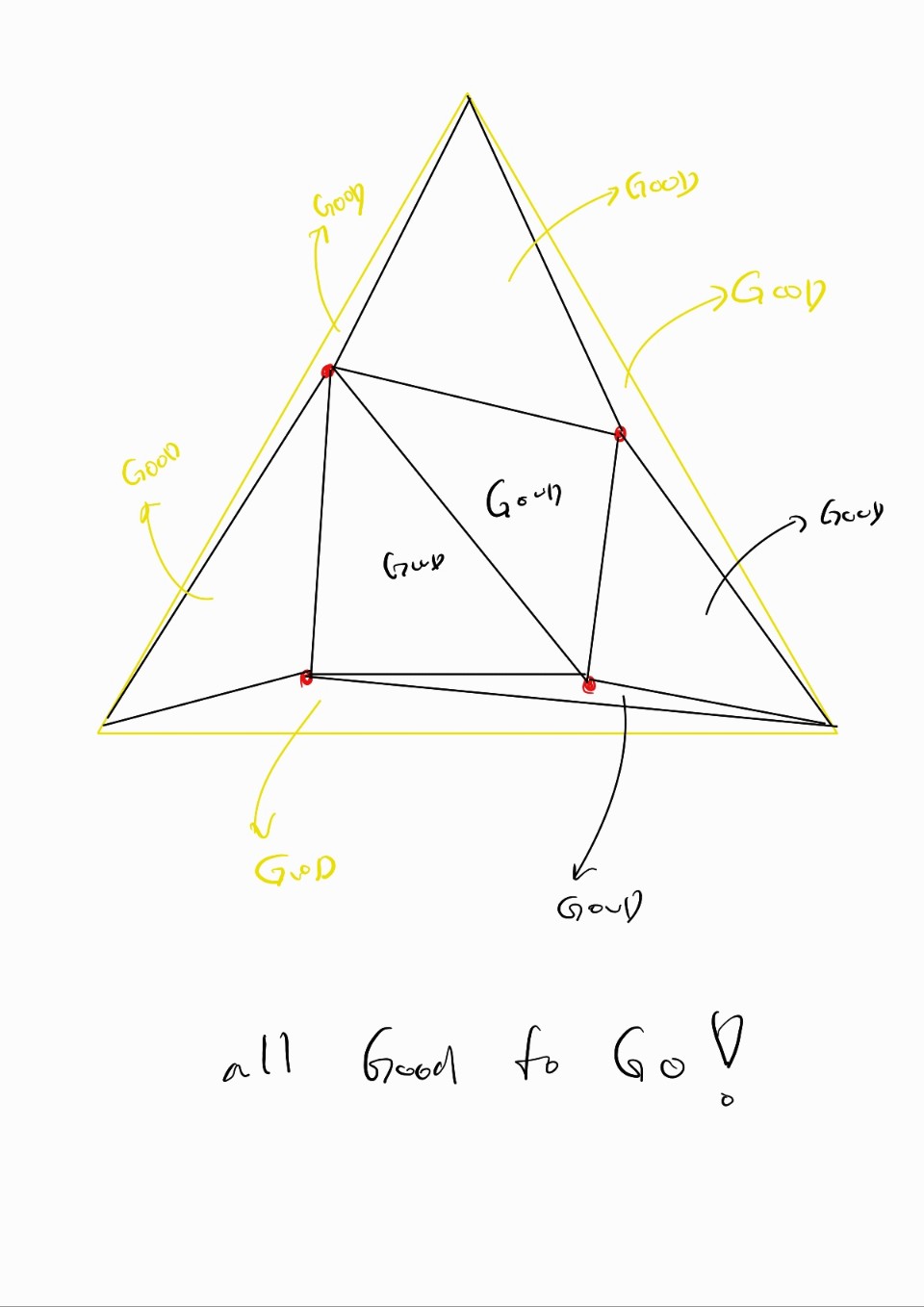
6. 이제 초기에 만들어줬던 Supertriangle은 제거해준다
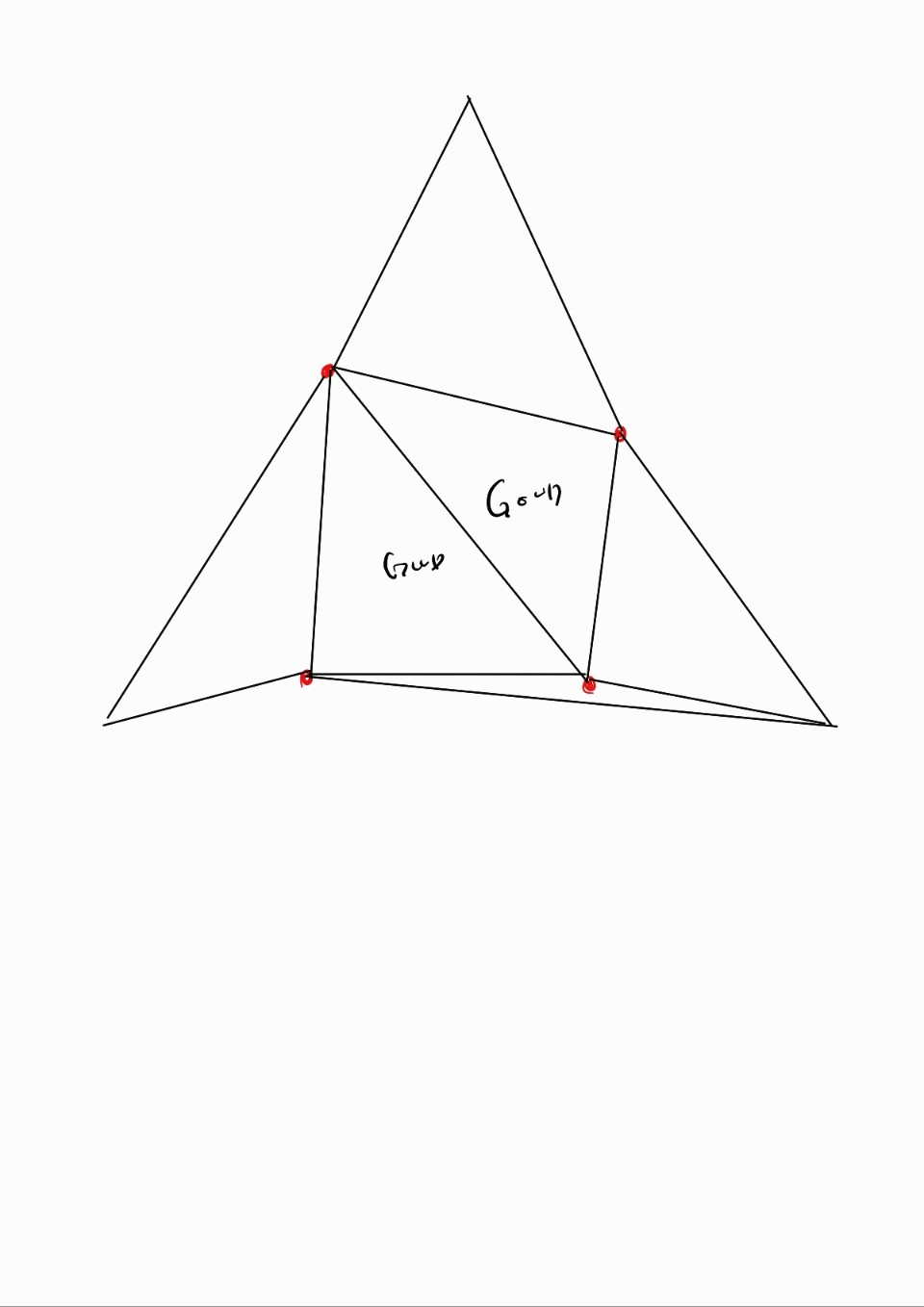
7. Super Triangle과 edge나 vertex를 공유했던 모든 삼각형도 제거 해준다
Vornoi Diagram
공간을 분할하고 분석하는 데 있어 보로노이 다이어그램과 들로네 삼각분할은 마치 동전의 양면과 같은 관계를 가집니다. 이 두 개념은 서로 밀접하게 연관되어 있으며, 공간 데이터를 다루는 다양한 분야에서 핵심적인 역할을 합니다.
보로노이 다이어그램부터 살펴보겠습니다. 이는 주어진 시드 점(seed point)들을 기준으로 평면을 분할하는 방법입니다. 각 영역은 해당 시드 점에 가장 가까운 점들의 집합으로 정의됩니다. 즉, 평면 위의 모든 점은 가장 가까운 시드 점에 따라 특정 영역에 속하게 됩니다. 이러한 특성 때문에 보로노이 다이어그램은 최근접 이웃 문제를 해결하는 데 매우 유용합니다.
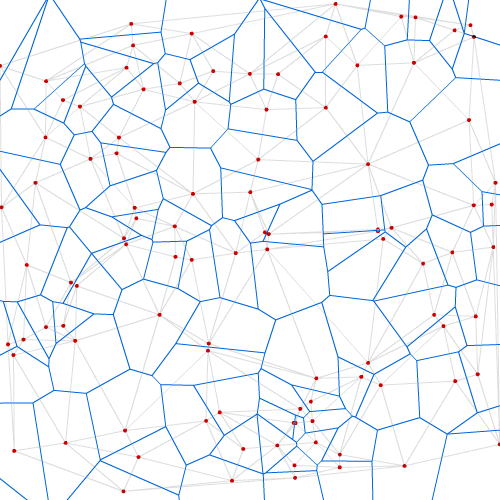
한편, 들로네 삼각분할은 이미 살펴본 바와 같이 주어진 점들을 연결하여 삼각형을 만드는 방법입니다. 그런데 이 두 개념이 서로 어떻게 연결될까요? 바로 여기서 '듀얼 이미지(dual image)' 관계가 등장합니다.
들로네 삼각분할과 보로노이 다이어그램은 서로의 듀얼 이미지입니다. 이는 한 방법에서 다른 방법으로 쉽게 변환할 수 있다는 것을 의미합니다. 구체적으로:
1. 들로네 삼각분할에서 보로노이 다이어그램으로:
- 들로네 삼각형들의 외접원 중심을 연결하면 보로노이 다이어그램이 됩니다.
- 특정 점을 공통 꼭지점으로 하는 모든 들로네 삼각형의 외접원 중심을 연결하면, 그 점을 시드로 하는 보로노이 영역이 만들어집니다.
2. 보로노이 다이어그램에서 들로네 삼각분할로:
- 인접한 보로노이 영역들의 시드 점들을 서로 연결하면 들로네 삼각분할이 됩니다.

이러한 듀얼 관계는 두 방법의 응용과 계산 알고리즘이 매우 유사하다는 것을 의미합니다. 실제로, 많은 경우 한 방법으로 문제를 해결하면 다른 방법으로도 동일한 문제를 해결할 수 있습니다.
이 듀얼 관계의 실제 응용은 매우 광범위합니다:
- 지리정보시스템(GIS)에서 공간 분석과 보간
- 컴퓨터 그래픽스에서의 메쉬 생성과 표면 재구성
- 로봇 공학에서의 경로 계획
- 생물학에서의 세포 구조 모델링
- 도시 계획에서의 서비스 영역 분석
결론적으로, 보로노이 다이어그램과 들로네 삼각분할은 공간을 이해하고 분석하는 데 있어 서로 보완적인 도구입니다. 이 두 개념의 듀얼 관계를 이해하면, 공간 데이터를 다루는 다양한 문제에 더욱 효과적으로 접근할 수 있습니다. 각 방법의 장점을 활용하고, 필요에 따라 두 방법을 자유롭게 전환하며 사용할 수 있다는 점은 공간 분석의 유연성과 효율성을 크게 높여줍니다.
Uses
Clustering
데이터 마이닝과 분류 작업에서 가장 도전적인 과제 중 하나는 주어진 데이터 분포에서 의미 있는 클러스터를 식별하는 것입니다. 특히 클러스터의 수를 사전에 알 수 없는 경우, 이 작업은 더욱 복잡해집니다. 그러나 들로네 삼각분할(Delaunay Triangulation)을 활용하면 이 문제에 효과적으로 접근할 수 있습니다. 이 방법은 간단하면서도 강력한 클러스터링 기법을 제공합니다.
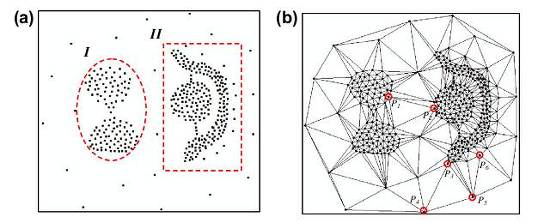
들로네 삼각분할을 이용한 클러스터링 과정은 다음과 같습니다:
1. 데이터 점들에 대해 들로네 삼각분할을 수행합니다.
2. 생성된 삼각형들 중 일정 길이 이상의 긴 변들을 제거합니다.
3. 남은 연결된 구성요소들을 각각의 클러스터로 간주합니다.
이 방법의 장점은 다음과 같습니다:
1. 클러스터의 형태에 대한 사전 가정이 필요 없습니다:
- 많은 전통적인 클러스터링 알고리즘들은 클러스터가 구형(spherical)이라고 가정하지만, 이 방법은 그러한 제약이 없습니다.
2. 클러스터의 수를 미리 지정할 필요가 없습니다:
- K-means 같은 알고리즘과 달리, 클러스터의 수를 자동으로 결정합니다.
3. 데이터의 밀도 변화에 잘 대응합니다:
- 데이터 밀도가 다양한 경우에도 효과적으로 작동합니다.
4. 노이즈 처리가 용이합니다:
- 긴 변을 제거하는 과정에서 자연스럽게 이상치(outlier)나 노이즈를 필터링할 수 있습니다.
5. 계산 효율성이 높습니다:
- 들로네 삼각분할은 효율적인 알고리즘이 존재하며, 이를 기반으로 한 클러스터링도 상대적으로 빠릅니다.
이 방법을 실제로 구현할 때 고려해야 할 몇 가지 사항이 있습니다:
1. 임계값 설정:
- "일정 길이 이상의 긴 변"을 정의하는 임계값을 어떻게 설정할 것인가? 이는 데이터의 특성과 원하는 클러스터의 세밀도에 따라 조정될 수 있습니다.
2. 고차원 데이터 처리:
- 2차원을 넘어서는 고차원 데이터의 경우, 들로네 삼각분할의 고차원 버전인 들로네 테셀레이션(Delaunay Tessellation)을 사용할 수 있습니다.
3. 대규모 데이터셋:
- 매우 큰 데이터셋의 경우, 전체 데이터에 대한 들로네 삼각분할이 계산적으로 부담될 수 있습니다. 이 경우 데이터를 분할하여 처리하는 방법을 고려할 수 있습니다.
들로네 삼각분할을 이용한 클러스터링은 복잡한 형태의 클러스터를 식별하는 데 특히 유용합니다. 예를 들어, 지리공간 데이터에서 자연적인 경계나 패턴을 찾거나, 이미지 분석에서 객체를 분할하는 데 효과적으로 사용될 수 있습니다.
이 방법은 전통적인 클러스터링 알고리즘들과 비교했을 때 특히 데이터의 구조적 특성을 잘 포착할 수 있다는 장점이 있습니다. 그러나 모든 상황에 완벽한 해결책은 아니며, 데이터의 특성과 분석 목적에 따라 다른 클러스터링 기법과 함께 보완적으로 사용되는 것이 좋습니다.
결론적으로, 들로네 삼각분할을 이용한 클러스터링은 데이터 과학자와 연구자들에게 강력하고 유연한 도구를 제공합니다. 이는 복잡한 데이터 구조를 이해하고 의미 있는 패턴을 추출하는 데 큰 도움이 될 수 있습니다.
Data Distribution Density
들로네 삼각분할(Delaunay Triangulation)의 응용 중 하나로, 평면상에 분포된 점들의 밀도를 수치화하는 방법이 있습니다. 이 방법은 Delaunay Tessellation Field Estimator (DTFE)라고 불리며, 특히 공간 데이터의 밀도 분석에 유용하게 사용됩니다. DTFE의 핵심 아이디어와 응용에 대해 자세히 살펴보겠습니다.
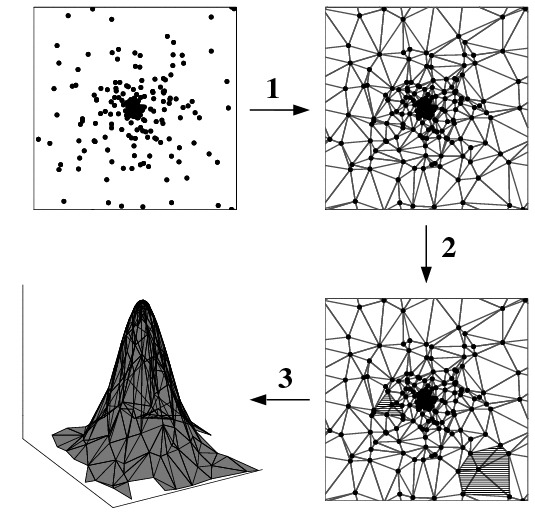
DTFE의 기본 원리:
1. 밀도 계산:
- 특정 점 p에서의 밀도는 p를 꼭지점으로 하는 주변 들로네 삼각형들의 면적 합의 역수로 정의됩니다.
- 밀도 = c / (s1 + s2 + ... + sk)
여기서 c는 상수, s1, s2, ..., sk는 점 p를 꼭지점으로 하는 들로네 삼각형들의 면적입니다.
2. 공간 전체 밀도 수치화:
- 개별 점에서 계산된 밀도 값들을 보간(interpolation)하여 전체 공간의 밀도를 추정합니다.
DTFE의 장점:
1. 동적 해상도:
- 데이터 분포에 따라 자동으로 해상도가 조정됩니다. 밀집된 영역에서는 더 높은 해상도의 밀도 추정이 가능합니다.
2. 모델 독립성:
- 기본 분포에 대한 가정이 필요 없어, 다양한 형태의 분포에 적용할 수 있습니다.
3. 경계 보존:
- 분포의 급격한 변화나 경계를 잘 포착할 수 있습니다.
4. 다차원 확장 가능:
- 2차원을 넘어 고차원 데이터에도 적용할 수 있습니다.
주요 응용 분야:
1. 천체물리학:
- DTFE의 주요 응용 분야로, 우주의 대규모 구조 분석에 사용됩니다.
- 은하의 분포, 암흑 물질의 밀도 추정 등에 활용됩니다.
2. 지리정보시스템(GIS):
- 지형 분석, 인구 밀도 매핑 등에 사용될 수 있습니다.
3. 생태학:
- 생물 종의 분포 패턴 분석에 활용될 수 있습니다.
4. 컴퓨터 비전:
- 이미지에서의 특징점 분포 분석에 사용될 수 있습니다.
- 객체 검출, 세그멘테이션 등의 작업에서 유용할 수 있습니다.
5. 머신러닝:
- 데이터 전처리 단계에서 특징 공간의 밀도를 분석하는 데 사용될 수 있습니다.
컴퓨터 비전에서의 잠재적 응용:
1. 텍스처 분석:
- 이미지의 텍스처를 특징점의 분포 밀도로 표현할 수 있습니다.
2. 객체 검출:
- 특징점의 밀도 분포를 이용해 객체의 경계나 중심을 추정할 수 있습니다.
3. 움직임 분석:
- 비디오 프레임에서 특징점의 밀도 변화를 추적하여 움직임을 분석할 수 있습니다.
4. 이미지 분할:
- 밀도 분포의 불연속점을 이용해 이미지를 의미 있는 영역으로 분할할 수 있습니다.
5. 관심 영역 검출:
- 높은 밀도를 가진 영역을 관심 영역으로 식별할 수 있습니다.
DTFE는 복잡한 공간 데이터의 분석에 강력한 도구가 될 수 있습니다. 특히 데이터의 분포가 불규칙하거나 다양한 스케일을 가질 때 유용합니다. 천체물리학에서 시작된 이 방법이 다른 분야, 특히 컴퓨터 비전 분야에서도 혁신적인 응용을 찾을 수 있을 것입니다.
이 방법의 한계점으로는 계산 복잡성과 대규모 데이터셋에 대한 메모리 요구사항이 있을 수 있습니다. 그러나 이러한 문제는 병렬 처리 기술이나 근사 알고리즘을 통해 일부 해결할 수 있습니다.
결론적으로, DTFE는 데이터 과학자와 연구자들에게 공간 데이터의 분포를 이해하고 분석하는 데 있어 강력하고 유연한 도구를 제공합니다. 이 방법의 다양한 분야로의 확장과 응용은 앞으로도 계속될 것으로 기대됩니다.
Convex Hull
https://tonnykang.tistory.com/229
컨벡스 헐(Convex Hull)은 계산 기하학에서 매우 중요한 개념입니다. 이는 주어진 점들의 집합을 모두 포함하는 가장 작은 볼록 다각형을 의미합니다. 쉽게 말해, 고무줄로 모든 점들을 감싸는 모양이라고 생각할 수 있습니다. 들로네 삼각분할(Delaunay Triangulation)을 이용해 컨벡스 헐을 구하는 방법은 매우 효과적이고 우아한 해결책을 제공합니다.
Convex Hull Problem 컨벡스 헐
Convex Hull은 점들의 집합이 있을때 이 모든 점들을 포함하는 크기가 최소인 Convex Polygon을 찾는 문제이다Convexity 쉽게 말해 위처럼 집합 내에 있는 두 점을 연결한 선분이 집합 내에 있어야Convex하
tonnykang.tistory.com
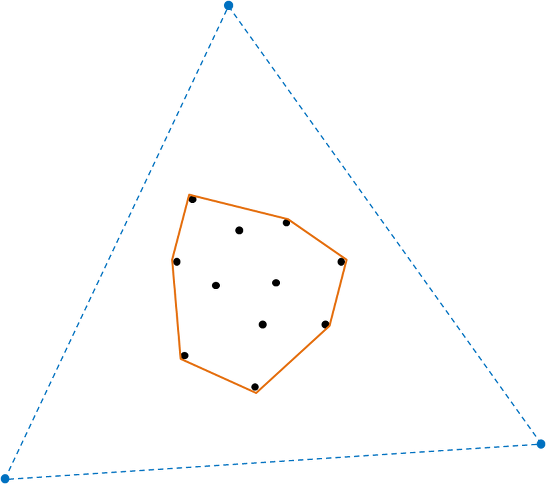
들로네 삼각분할을 이용한 컨벡스 헐 구하기:
1. 외부 점 추가:
- 원래 점들의 집합 외부에 3개의 점을 추가합니다.
- 이 외부 점들은 원래의 모든 점들을 포함할 수 있을 만큼 충분히 멀리 위치해야 합니다.
2. 들로네 삼각분할 수행:
- 원래의 점들과 추가된 외부 점들을 모두 포함하여 들로네 삼각분할을 수행합니다.
3. 외부 점과 연결된 점들 식별:
- 새로 추가된 외부 점들과 삼각형을 이루는 원래 점들을 찾습니다.
4. 컨벡스 헐 구성:
- 식별된 점들을 연결하면 원래 점들의 집합에 대한 컨벡스 헐이 완성됩니다.
이 방법의 장점:
1. 효율성:
- 들로네 삼각분할은 O(n log n) 시간 복잡도를 가지므로, 대규모 점 집합에 대해서도 효율적입니다.
2. 정확성:
- 수학적으로 정확한 컨벡스 헐을 보장합니다.
3. 추가 정보:
- 컨벡스 헐뿐만 아니라 점들 간의 연결 관계도 얻을 수 있어, 추가적인 분석에 유용합니다.
4. 강건성:
- 외부 점을 사용함으로써 특이 케이스(예: 모든 점이 일직선 상에 있는 경우)도 쉽게 처리할 수 있습니다.
구현 시 고려사항:
1. 외부 점 선택:
- 외부 점들은 모든 원래 점들을 포함할 수 있을 만큼 충분히 멀리 위치해야 합니다.
- 일반적으로 원래 점들의 경계를 크게 벗어나는 위치에 삼각형 형태로 배치합니다.
2. 수치 안정성:
- 매우 큰 좌표값을 사용할 경우 수치 오차에 주의해야 합니다.
3. 특이 케이스 처리:
- 모든 점이 일직선상에 있는 경우 등의 특이 케이스를 고려해야 합니다.
응용 분야:
1. 컴퓨터 그래픽스:
- 객체의 경계 표현, 충돌 검출 등에 사용됩니다.
2. 패턴 인식:
- 객체의 형태 분석에 활용됩니다.
3. 지리정보시스템(GIS):
- 지형 분석, 영역 경계 설정 등에 사용됩니다.
4. 로봇 공학:
- 장애물 회피, 경로 계획 등에 활용됩니다.
5. 데이터 마이닝:
- 이상치 검출, 클러스터 분석 등에 사용됩니다.
들로네 삼각분할을 이용한 컨벡스 헐 구하기 방법은 기하 알고리즘의 아름다움을 잘 보여주는 예입니다. 이 방법은 단순히 컨벡스 헐을 구하는 것을 넘어서, 점들 간의 관계와 공간 구조에 대한 풍부한 정보를 제공합니다.
이 접근 방식은 특히 컨벡스 헐 외에도 추가적인 기하학적 정보가 필요한 경우에 유용합니다. 예를 들어, 점 집합의 내부 구조나 근접성 관계 등을 분석해야 하는 경우, 들로네 삼각분할을 통해 얻은 정보를 추가로 활용할 수 있습니다.
결론적으로, 들로네 삼각분할을 이용한 컨벡스 헐 구하기는 효율성, 정확성, 그리고 추가 정보 제공이라는 여러 장점을 동시에 얻을 수 있는 강력한 방법입니다. 이는 계산 기하학의 다양한 문제를 해결하는 데 있어 핵심적인 도구로 자리 잡고 있으며, 앞으로도 다양한 분야에서 그 활용도가 더욱 확대될 것으로 기대됩니다.
'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| Pre Order Post Order Tree Traversal 전위 후위 순회 (2) | 2025.02.08 |
|---|---|
| 알고리즘 배열의 기본 개념 (1) | 2025.01.17 |
| 백준 11723 파이썬 "집합" (1) | 2024.08.04 |
| 백준 1697번 숨바꼭질 파이썬 (4) | 2024.07.10 |
| Genetic Algorithm 유전 알고리즘 (38) | 2024.06.13 |