유니온-파인드(Union-Find, 서로소 집합 또는 분리 집합 Disjoint set이라고도 함)는 여러 개의 서로소 집합으로 나누어진 원소들을 추적하는 자료구조입니다. 주요 연산은 다음 두 가지입니다:
- 파인드(Find): 특정 원소가 어느 집합에 속하는지 판별합니다. 두 원소가 같은 집합에 속하는지 확인하는 데 사용됩니다.
- 유니온(Union): 두 개의 집합을 하나의 집합으로 합칩니다.
유니온-파인드의 핵심 구성 요소
- 부모 배열: parent[] 배열로, parent[i]는 원소 i의 부모를 저장합니다. 초기에는 각 원소가 자신을 부모로 가집니다(자기 자신이 루트).
- 랭크/크기 배열: rank[] 또는 size[] 배열로, 유니온 수행 시 트리의 균형을 맞추어 성능 저하를 일으킬 수 있는 극단적인 경우를 피하는 데 도움을 줍니다.
유니온-파인드 연산
- 초기화
parent = [i for i in range(n)] # 초기에 각 원소는 자신이 부모
rank = [0] * n # 모든 원소의 랭크(또는 깊이)는 0
2. 파인드 연산 (경로 압축 포함)목표: 원소가 속한 집합의 루트를 찾습니다.
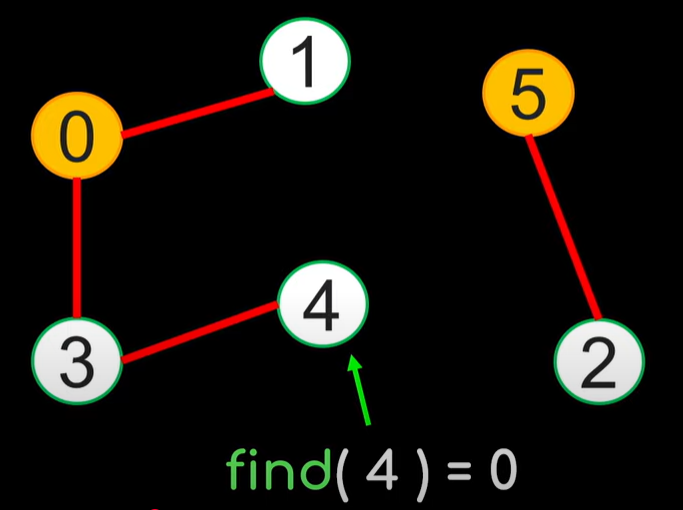
경로 압축 없이:
def find(x):
if parent[x] == x:
return x
return find(parent[x])
왜 부모를 찾는게 이렇게 단순한지 의구심이 들 수 있는데
트리 형태로 아래와 같이 두면
Root노드의 Parent는 자기자신이다
라는 주요 규칙만 따라주면 됨을 알 수 있다

그래서 그 규칙에 의하면,
나중에 Union 함수를 구현 할 때에도
두개의 Root중 내가 더 우선순위가 높다 설정한 놈을 올리고
나머지 Root노드 (이제는 아니게된)의 Parent node를 새로운 Root 노드로 업데이트 하면 된다

경로 압축 포함:
- find 연산 중에 각 노드를 루트에 직접 연결하여 향후 연산을 위해 구조를 편하게 만듭니다.
def find(x):
if parent[x] != x:
parent[x] = find(parent[x]) # 경로 압축
return parent[x]
3. 유니온 연산 (랭크/크기에 의한 합집합 포함)목표: 루트들을 연결하여 두 집합을 병합합니다.

- 랭크에 의한 합집합:
- 작은 트리를 큰 트리의 루트 아래에 붙입니다.
- 크기에 의한 합집합:
- 원소가 적은 트리를 원소가 많은 트리 아래에 붙입니다.
def union(a, b):
rootA = find(a)
rootB = find(b)
if rootA != rootB:
if rank[rootA] < rank[rootB]:
parent[rootA] = rootB
elif rank[rootA] > rank[rootB]:
parent[rootB] = rootA
else:
parent[rootB] = rootA
rank[rootA] += 1
랭크 배열이 필요한 이유랭크 배열(또는 크기 배열)은 각 집합을 나타내는 트리의 깊이(또는 높이)를 추적하는 데 사용됩니다. 그 목적은 유니온 연산을 수행할 때 트리를 얕게 유지하는 것입니다.
두 집합을 병합할 때, 트리가 불필요하게 깊어지는 것을 피하고자 합니다. 깊은 트리는 find 연산이 더 느려지기 때문입니다. 얕은 트리를 깊은 트리 아래에 붙임으로써 전체 구조의 균형을 더 잘 유지할 수 있습니다.
퇴화 트리 또는 편향 트리란? (Degenerate or Skewed Trees)
퇴화 트리(또는 편향 트리)는 트리 구조가 매우 불균형하여 연결 리스트와 비슷한 형태가 되는 경우입니다. 이는 원소들이 항상 한 줄로 연결될 때 발생하며, 깊이가 O(N)이 됩니다.

퇴화 트리의 예시(랭크나 경로 압축 없이) 다음과 같은 순서로 유니온을 수행하면:
Union(0, 1)
Union(1, 2)
Union(2, 3)
Union(3, 4)
결과는 다음과 같습니다:
0 -> 1 -> 2 -> 3 -> 4
이 경우 find(4)는 모든 노드를 거쳐야 합니다 4 -> 3 -> 2 -> 1 -> 0, 최악의 경우 O(N) 시간 복잡도가 됩니다.
랭크 배열은 어떻게 도움이 되나요?
랭크 배열은 다음을 보장하여 퇴화 트리를 방지합니다:
- 낮은 랭크의 트리가 높은 랭크의 트리 아래에 붙습니다.
- 두 트리의 랭크가 같은 경우, 새로운 루트의 랭크를 증가시킵니다. 이를 통해 트리 높이를 가능한 한 작게 유지하여 더 효율적인 연산이 가능해집니다.
랭크와 크기의 차이
- 랭크: 트리의 높이를 추적합니다.
- 크기: 트리의 원소 개수를 추적합니다. 둘 다 균형을 유지하는 데 사용되지만, 랭크는 깊이를 기준으로, 크기는 전체 노드 수를 기준으로 합니다.
랭크/크기가 없는 경우
- 최악의 경우 시간 복잡도가 **O(N)**까지 저하될 수 있습니다.
랭크/크기 사용 시(경로 압축 포함):
- 시간 복잡도가 O(α(N))(거의 상수 시간)으로 개선되어 유니온-파인드가 매우 효율적이 됩니다.
시간 복잡도 분석
- 최적화 없는 최악의 경우: 연산당 O(N)
- 경로 압축과 랭크에 의한 합집합 포함: O(α(N)) (애커만 함수의 역함수), 실질적으로 상수 시간
예제 단계별 설명 5개의 원소를 가진 집합을 고려해봅시다: {0, 1, 2, 3, 4}
- 초기 상태:
parent: [0, 1, 2, 3, 4]
rank: [0, 0, 0, 0, 0]
2. Union(0, 1):
parent: [0, 0, 2, 3, 4]
rank: [1, 0, 0, 0, 0]
3. Union(1, 2):
parent: [0, 0, 0, 3, 4]
rank: [1, 0, 0, 0, 0]
4. Find(2):
- 경로 압축이 발생합니다. 2의 부모가 0이 되어 2를 0에 직접 연결합니다.
parent: [0, 0, 0, 3, 4]
실수하기 쉬운 내용들
- 경로 압축을 수행하지 않으면 편향된 트리가 생성되어 연산이 느려질 수 있습니다.
- 랭크/크기에 의한 합집합 없이 병합하면 깊은 트리가 생성되어 연산이 비효율적이 될 수 있습니다.
코딩 테스트에서 유니온-파인드가 중요한 이유
- 효율성: 유니온-파인드는 경로 압축과 랭크/크기에 의한 합집합을 구현하면 매우 효율적입니다. 각 연산의 분할 상환 시간복잡도는 거의 O(α(N))입니다. 여기서 α(N)는 애커만 함수(Ackerman)의 역함수로, 실제 사용되는 모든 입력 크기에 대해 거의 상수 시간이 걸립니다.
- 그래프 문제에서 자주 사용: 많은 코딩 문제, 특히 그래프 관련 문제들은 연결 요소와 관련된 연산을 효율적으로 처리하기 위해 유니온-파인드를 사용합니다.
- 단순성과 유용성: 구현이 비교적 쉽고, 경쟁 프로그래밍에서 자주 등장하므로 숙달해야 할 중요한 도구입니다.
유니온-파인드가 사용되는 일반적인 문제 유형들
- 그래프의 연결 요소:
- 두 정점이 같은 연결 요소에 속하는지 확인
- 연결 요소의 개수 세기
- 무방향 그래프에서 사이클 (Cycle) 탐지:

Cycle, https://media.geeksforgeeks.org/wp-content/uploads/20230306153646/cyclic-graphdrawio.png - 간선에 대해 유니온 연산을 수행하고 두 정점이 이미 같은 부모를 공유하는지 확인하여 사이클을 탐지
- 크루스칼 알고리즘(최소 신장 트리) Kruskal's Algorithm (Minimal Spanning Tree):

- 간선 추가가 사이클을 형성하는지 효율적으로 확인하기 위해 유니온-파인드가 필수적
- 동적 연결성:
- 간선 추가로 인해 연결성이 동적으로 변할 때 연결성을 효율적으로 유지하고 조회
- 침투 문제:
- 다공성 물질을 통한 유체 흐름을 시뮬레이션하며 주로 유니온-파인드로 해결
- 방정식 가능성 문제(Leetcode 990):
- 주어진 변수들 간의 등식과 부등식 관계가 동시에 만족될 수 있는지 판단
기억해야 할 핵심 개념
- 경로 압축: 집합을 나타내는 트리를 더 평평하게 만들어 각 노드가 루트를 직접 가리키게 합니다.
- 랭크/크기에 의한 합집합: 항상 작은 트리를 큰 트리의 루트 아래에 붙여 트리를 얕게 유지합니다.
예제 문제들
- 그래프의 연결 요소
- 무방향 그래프에서의 사이클 탐지
- 방정식 가능성 여부 (Leetcode 990)
1. Python에서의 유니온-파인드 클래스
먼저 경로 압축과 랭크에 의한 합집합을 사용하여 트리의 균형을 유지하는 유니온-파인드 클래스를 구현하겠습니다:
class UnionFind:
def __init__(self, n):
# 각 원소는 처음에 자신만의 집합에 속합니다.
self.parent = list(range(n))
self.rank = [0] * n # 트리를 얕게 유지하는 데 사용됩니다.
def find(self, x):
# x를 포함하는 집합의 루트(대표)를 찾습니다.
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x]) # 경로 압축
return self.parent[x]
def union(self, x, y):
# x와 y를 포함하는 집합들을 합칩니다.
rootX = self.find(x)
rootY = self.find(y)
if rootX == rootY:
return # 이미 같은 집합에 속해 있습니다.
# 랭크에 의한 합집합: 더 낮은 트리를 더 높은 트리 아래에 붙입니다.
if self.rank[rootX] < self.rank[rootY]:
self.parent[rootX] = rootY
elif self.rank[rootX] > self.rank[rootY]:
self.parent[rootY] = rootX
else:
self.parent[rootY] = rootX
self.rank[rootX] += 1
이 클래스는 효율적인 find와 union 연산을 제공합니다.
2. 그래프의 연결 요소
문제 설명
- 두 정점이 같은 연결 요소에 속하는지 확인하기: find 메서드를 사용하여 두 정점이 같은 루트를 가지는지 확인합니다.
- 연결 요소의 개수 세기: 모든 간선을 처리한 후 고유한 루트의 개수를 셉니다.
예제 코드
def count_components(n, edges):
"""
n: 정점의 수 (0부터 n-1까지 레이블이 붙음)
edges: 무방향 간선의 리스트, 각 간선은 (u, v) 튜플
"""
uf = UnionFind(n)
# 각 간선에 대해 정점들을 합칩니다.
for u, v in edges:
uf.union(u, v)
# 집합을 사용하여 고유한 루트를 셉니다.
unique_roots = set()
for i in range(n):
unique_roots.add(uf.find(i))
return len(unique_roots)
# 사용 예시:
n = 5
edges = [(0, 1), (1, 2), (3, 4)]
print("연결 요소의 개수:", count_components(n, edges))
# 2개의 연결 요소가 출력됨: {0,1,2}와 {3,4}
설명:
- n개의 노드에 대한 UnionFind 인스턴스를 생성합니다.
- 각 간선에 대해 두 정점을 합칩니다.
- 마지막으로 모든 정점을 순회하며 대표(루트)를 수집합니다. 고유한 루트의 개수가 연결 요소의 개수가 됩니다.
3. 무방향 그래프에서의 사이클 탐지
문제 설명
- 무방향 그래프에서 이미 같은 루트를 공유하는 두 정점을 합치려고 하면, 해당 간선을 추가하면 사이클이 형성됩니다.
예제 코드
def has_cycle(n, edges):
"""
n: 정점의 수
edges: 무방향 간선의 리스트, 각 간선은 (u, v) 튜플
"""
uf = UnionFind(n)
for u, v in edges:
# u와 v가 이미 연결되어 있다면, 이 간선을 추가하면 사이클이 생성됩니다.
if uf.find(u) == uf.find(v):
return True
uf.union(u, v)
return False
# 사용 예시:
n = 4
edges_with_cycle = [(0, 1), (1, 2), (2, 0), (2, 3)]
edges_without_cycle = [(0, 1), (1, 2), (2, 3)]
print("사이클 탐지 (True여야 함):", has_cycle(n, edges_with_cycle))
print("사이클 탐지 (False여야 함):", has_cycle(n, edges_without_cycle))
설명:
- 각 간선에 대해 먼저 find를 사용하여 두 끝점이 이미 같은 집합에 있는지 확인합니다.
- 만약 그렇다면, 사이클이 탐지된 것입니다.
- 아니라면, 두 정점을 합치고 계속 진행합니다.
4. 방정식 가능성 여부 (Leetcode 990)
문제 설명
- 방정식을 나타내는 문자열 배열("a==b" 또는 "a!=b" 형태)이 주어졌을 때, 모든 방정식을 만족하도록 변수에 값을 할당할 수 있는지 판단합니다.
- 1단계: "=="가 있는 모든 방정식을 처리하고 해당하는 변수들을 합칩니다.
- 2단계: "!="가 있는 모든 방정식을 처리하고 불평등이 위반되는지 확인합니다(즉, 두 변수가 같은 루트를 가지는지).
예제 코드
def equations_possible(equations):
"""
equations: 방정식을 나타내는 문자열 리스트, 예: "a==b", "b!=c"
"""
# 가능한 소문자는 26개입니다.
uf = UnionFind(26)
# 1단계: "=="가 있는 모든 방정식에 대해 합집합 수행
for eq in equations:
if eq[1:3] == "==":
x = ord(eq[0]) - ord('a')
y = ord(eq[3]) - ord('a')
uf.union(x, y)
# 2단계: "!="가 있는 모든 방정식 확인
for eq in equations:
if eq[1:3] == "!=":
x = ord(eq[0]) - ord('a')
y = ord(eq[3]) - ord('a')
if uf.find(x) == uf.find(y):
# 충돌 발견: 같지 않아야 할 두 변수가 연결되어 있습니다.
return False
return True
# 사용 예시:
equations1 = ["a==b", "b==c", "a==c"]
equations2 = ["a==b", "b!=c", "c==a"]
print("방정식 가능 (True여야 함):", equations_possible(equations1))
print("방정식 가능 (False여야 함):", equations_possible(equations2))
설명:
- 합집합 단계: 먼저 같다고 선언된 모든 변수들을 합칩니다.
- 검증 단계: 그 다음, 각 불평등에 대해 두 변수가 같은 집합에 있는지 확인합니다. 만약 그렇다면 방정식들을 만족시킬 수 없습니다.
요약
- 연결 요소: 유니온-파인드를 사용하여 노드들을 병합하고 고유한 루트를 셉니다.
- 사이클 탐지: 합집합 연산 중에 끝점들이 이미 연결되어 있는지 확인합니다.
- 방정식 가능성 여부: 먼저 같은 변수들을 합치고, 그 다음 불평등이 합집합과 충돌하지 않는지 확인합니다.
'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| [프로그래머스] 다단계 칫솔 판매 파이썬 풀이 (0) | 2025.02.13 |
|---|---|
| Pre Order Post Order Tree Traversal 전위 후위 순회 (2) | 2025.02.08 |
| 알고리즘 배열의 기본 개념 (1) | 2025.01.17 |
| 들로네 삼각분할 알고리즘과 보르노이 맵 (6) | 2024.09.07 |
| 백준 11723 파이썬 "집합" (1) | 2024.08.04 |