P, NP, NP-hard, NP-complete 문제의 이해
컴퓨터 과학에서 가장 중요한 개념 중 하나인 P, NP, NP-hard, NP-complete 문제.
이 개념들은 알고리즘의 효율성과 문제의 복잡성을 이해하는 데 핵심적이다.

이 글에서는 각 개념을 자세히 살펴보겠습니다.
P Problems (Polynomial)
P 문제는 결정론적 튜링 기계(deterministic Turing machine)로 다항 시간(Polynomial Time) 내에 해결할 수 있는 문제이다
결정론적 알고리즘: 특정 입력이 주어지면 항상 같은 출력을 예측 가능한 단계 순서로 생성하는 알고리즘이다\
즉 Heuristic한 알고리즘은 결정론적이지 않은 비결정론적 알고리즘이라고 할 수 있다
다항 시간: 알고리즘의 시간 복잡도가

인 경우, 여기서 n은 입력의 크기이고 k는 상수이다.
예를 들어, 알고리즘이 O(n^2) 또는 O(n^3) 시간을 소요한다면, 이는 다항 시간으로 간주된다
NP Problems (Non-Polynomial)
NP 문제는 비결정론적 알고리즘(Non-Deterministic Algorithm)으로 해결할 수 있으며,
문제의 해답이 있는지 여부를 다항 시간 내에 확인할 수 있는 문제이다.
비결정론적 알고리즘: 개념적으로, 여러 가능한 해답을 동시에 탐색하고 다항 시간 내에 해답을 "추측"할 수 있는 알고리즘입니다.
Optimal하지않은 솔루션을 도출하는 알고리즘은 전부 비결정론적이라고 할 수 있다
P와 NP의 관계
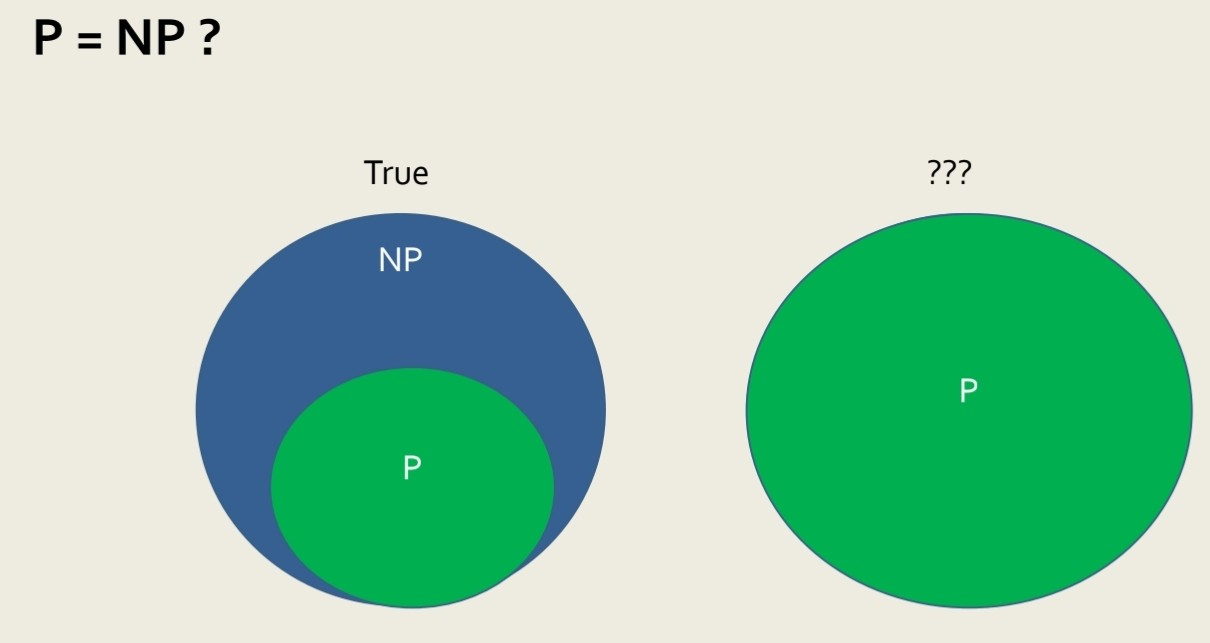
- P ⊆ NP: P에 속한 모든 문제는 NP에도 속한다. 왜냐하면 문제가 다항 시간 내에 해결될 수 있다면, 그 해답은 당연히 다항 시간 내에 확인될 수 있기 때문이다.
- P ?= NP인지 여부는 아직 해결되지 않은 문제이다. 만약 P = NP라면, 다항 시간 내에 해답을 확인할 수 있는 모든 문제가 다항 시간 내에 해결될 수 있다는 의미이기 때문이다. 이는 컴퓨터 과학에서 가장 큰 미해결 문제 중 하나이다.
Halting Problem
Alan Turing에 의해 증명된 문제인데
어떠한 컴퓨터 프로그램과, Input이 주어졌을때
이 프로그램은 무한으로 작동하는지 끝이 나는지 판별하는 프로그램의 존재를 찾는 문제이다
아래와 같이 isHalt() 라는 함수가 있다고 하자
이 함수는 어떠한 프로그램이 계속 작동하는지 멈추는지 판단하는 함수이다
Nonsense(){
if(isHalt(Nonsense()))
then while(true) do something;
}위와 같이 Nonsense()라는 함수가 있다
위와 같이 정의되어있으면
1. isHalt(nonsense()): True
nonsense()함수가 멈췄다는 뜻 <->근데 while() 걸려서 사실 무한 으로 돎
2. isHalt(nonsense()): False
nonsense()함수가 계속 돌아간다는 뜻 <-> 근데 if(isHalt(Nonsesnse))가 false라서 종료됨
그래서 논리적으로 존재 불가!
NP-Hard 문제
모든 NP 문제가 다항 시간 내에 해당 문제로 축소될 수 있다면, 그 문제는 NP-Hard이.
비공식적으로 말하자면, NP-Hard 문제는 NP에서 가장 어려운 문제만큼 최소한 어렵다는 의미이다.
NP-Complete 문제
문제가 다음 두 조건을 만족하면 NP-Complete이다
- NP에 속함 (해답을 다항 시간 내에 확인할 수 있음)
- NP-Hard임 (모든 NP 문제가 다항 시간 내에 해당 문제로 축소될 수 있음) Reduction!

NP-Complete 문제는 NP 내에서 가장 어려운 문제들이다
만약 어느 한 NP-Complete 문제라도 다항 시간 내에 해결될 수 있다면, NP의 모든 문제가 다항 시간 내에 해결될 수 있습니다. 이게 가능하면 P=NP임을 증명한다.

이는 증명되지는 않았지만! 또한 P문제는 NP에 속하지 않음도 증명되지 않았음.
또 모든 NP-Complete 문제들은
서로서로 Polynomial time 내에 Transform가능하기 때문에 한개만 증명해도 되는것이다
이 변환이 와닫지 않을것이기에 더 살펴보자
Transformation
problem A : 정수들의 집합 S가 있고 S의 부분집합의 합이 K인 부분집합을 찾는 문제
ex)
we have S={20, 35, 45, 70, 80} and k=105

{35,70}
Problem B : 같은 집합 S을 합이 같은 두개의 부분집합으로 나누는 문제
ex)
X={20, 35, 70} =125
Y={45, 80} =125
add t to S where s is the sum of S and

so basically we get a new set

and if we perform problem B on S’
the new solution sets X’ and Y’ sums sould be

because the sum of the new set S’ is

그러면 S의 두 부분집합 X', Y'이 있으면
이 부분집합 중 하나는 t를 포함할 것이다
그럼 t를 포함한 어떤 집합에 t를 빼주면
그 집합의 합은 K이가 될것이다!

위와 같이 Polynomial 시간 안에 문제A는 문제B로 전환될 수 있다
이렇게 모든 NP-Complete 문제들은 서로끼리 전환가능하다->Polynomial 시간 안에
'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| 백준 1697번 숨바꼭질 파이썬 (4) | 2024.07.10 |
|---|---|
| Genetic Algorithm 유전 알고리즘 (38) | 2024.06.13 |
| Convex Hull Problem 컨벡스 헐 (35) | 2024.06.09 |
| String Matching Algorithms 문자열 매칭 알고리즘 (33) | 2024.06.08 |
| A* 알고리즘 (Dijkstra algorithm) (23) | 2024.06.06 |