문자열 처리는 컴퓨터 과학과 프로그래밍에서 매우 중요한 주제이다.
특히, 특정 패턴을 텍스트 내에서 찾는 'Exact String Matching' 문제는 자주 등장하고 많은 분야에 활용된다.
- Exact String Matching
- 목표: 텍스트 문자열 T 내에서 패턴 문자열 P의 모든 출현 위치를 찾는 것.
- 예: T = "AGCTTGAGCTTGA", P = "GCTTGA"라면, P는 T에서 두 번 index 1, 7에서 나타난다
- 부분 문자열 (Substring) vs Subsequence
- 부분 문자열(Substring):
- 원 문자열의 연속된 부분.
- S{i,j}=Si,S{i+1}...Sj
- 예: S = "AGCTTGA"일 때, "GCT"는 부분 문자열.
- 부분 수열(Subsequence):
- 원 문자열에서 몇 개의 문자를 삭제하여 얻은 수열.
- S{i,j}=SiS{i+1}...Sj
- 예: S = "AGCTTGA"일 때, "ACT"와 "GCTT"는 부분 수열.
- 부분 문자열(Substring):
- 접두사와 접미사
- 접두사(Prefix):
- 문자열의 시작부터 시작하는 부분 문자열.
- 표기법: S{0,k}
- 예: S = "AGCTTGA"일 때, "AGC"는 접두사.
- 접미사(Suffix):
- 문자열의 끝으로 끝나는 부분 문자열.
- 표기법:S_{k,|S|} (|S|는 S의 길이)
- 프로그래머들은 종종 0부터 시작하는 인덱스를 사용합니다.
- 예: S = "AGCTTGA"일 때, "TGA"는 접미사.
- 접두사(Prefix):
- 브루트-포스(Brute-Force) 알고리즘
- 가장 단순한 접근법으로, 텍스트의 모든 위치에서 패턴과 일치하는지 확인.
- 시간 복잡도: O(mn) (m: 패턴의 길이, n: 텍스트의 길이)
- 문제점: 텍스트와 패턴이 길어질수록 실행 시간이 급격히 증가.
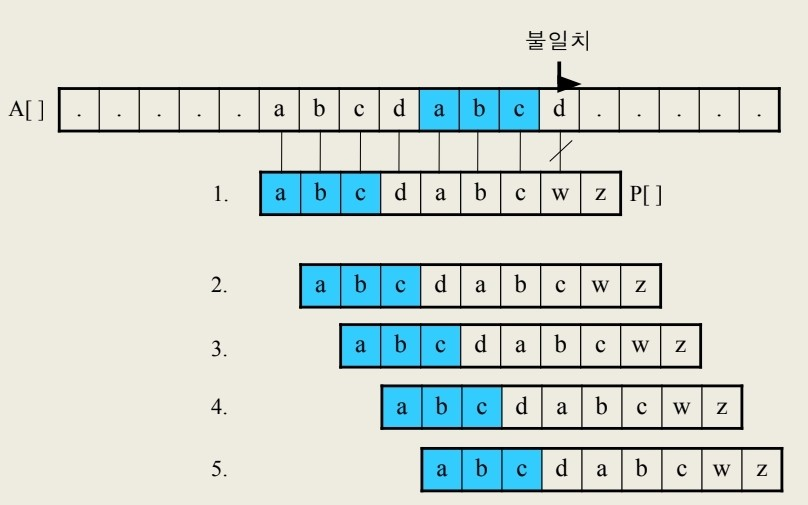
브루트-포스 알고리즘은 작은 문자열에는 충분하지만, 큰 데이터셋에는 비효율적이다. <위와 같은 경우>
이러한 한계를 극복하기 위해, 더 효율적인 알고리즘들이 개발되었다.
오토마타 Automata 활용
오토마타 같은 상태 머신을 활용해 스트링을 활용 하면 조금 더 개선된
효율적인 검사를 할 수 있다
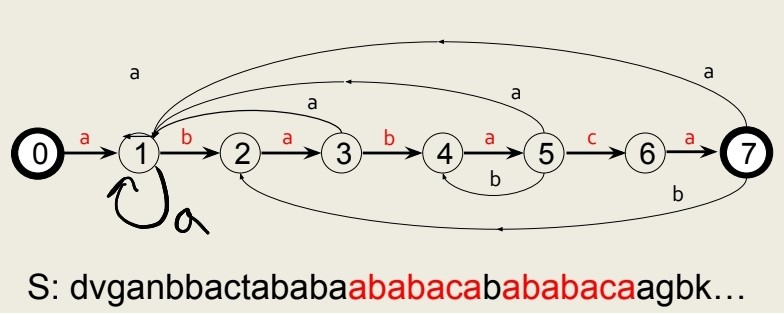
알파벳이 Σ 이면 -> 등장하는 모든 char의 종류, 복잡도는

그래서 더 효율적인 알고리즘들이 등장하는데
Rabin-Karp Algorithm
문자열 값들을 숫자값으로 변환시켜 문자열의 비교가 아닌 숫자들의 (보통 정수) 비교로 문제를 취급하는 방식이다
ex)
Σ={a,b,c,d,e}
|Σ|=5
so a,b,c,d,e are given values 0,1,2,3,4
and “cad” would be 28=25^2+05+35^0
하지만 string 값들을 정수형으로 변환하는데 상당한 과부하가 있다 Overhead!
O(m)의 시간정도 걸리고
패턴 P를 비교하는데에는 O(|T|m) 정도 걸린다
basicRabinKarp(A, P, d, q){
p=0, a1=0;
for i=0 to m{
p=d*p+p[i];
a1=d*a1+A[i];
}
for i=0 to n-m+1{
if i!=1 :
ai=d(a{i-1} - d^{m-1}*A[i-1])+A[i+m-1];
if p==ai:
MATCHED AT A[i];
}
}
위 Pseudocode를 살펴보면

A[i-1]: 창문 (widow)를 빠져나가는 character에 값을 뺴준다->이전에 가장 앞 문자
->d를 곱해주면 window를 오른쪽으로 한칸 당겨준다
A[i+m-1]: 새로 window에 들어오는 값들을 더해준다
하지만 여기서 알파벳 Σ 이 커지거나 패턴P의길이가 커지면
d가 exponentioal 하게 증가하기 떄문에 Overflow를 초래하기 쉽상이다
그래서 값을 1:1로 맞는지 확인하는 방법 말고
적당히 큰 소수 q값의 modulus 값을 비교하는 방법을 택한다
-> modulus가 같은 값들은 여러개 있을 수 있음
->그래서 modulus 값이 같은지 먼저 확인하고 그 후 string이 일치하는지 한번더 확인해줘야한
basicRabinKarp(A, P, d, q){
p=0, a1=0;
for i=0 to m{
p=d*p+p[i] mod q;
a1=d*a1+A[i] mod q;
}
for i=0 to n-m+1{
if i!=1 :
ai=d(a{i-1} - d^{m-1}*A[i-1])+A[i+m-1] mod q;
if p==ai:
if P[1:m]==A[i:i+m+1]:
MATCHED AT A[i];
}
}KMP Knuth-Morris-Pratt Algorithm
위에서 살펴본 오토마타 접근법과 매우 비슷하다
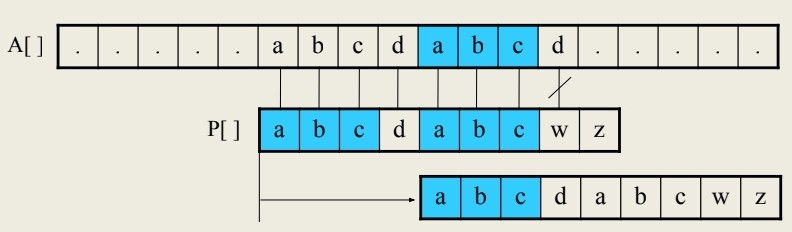
패턴 P내에서 어디서 틀렸는지에 따라서
바로 한칸 당겨서 비교하면 비효율적이니 비교할 필요 없는 곳들을 생략해
SP[]에 어디부터 다음 비교할지 저장해두는 방법을 활용한다
EX)
Text: ABABDABACDABABCABAB Pattern: ABABCABAB
Step 1: Preprocess the pattern to create the LPS array.
Pattern: A B A B C A B A B
LPS Array: 0 0 1 2 0 1 2 3 4
- lps[0] = 0 (no proper prefix which is suffix)
- lps[1] = 0 (no proper prefix which is suffix)
- lps[2] = 1 (A)
- lps[3] = 2 (AB)
- lps[4] = 0 (no proper prefix which is suffix)
- lps[5] = 1 (A)
- lps[6] = 2 (AB)
- lps[7] = 3 (ABA)
- lps[8] = 4 (ABAB)
SP[ ] 값 구하기
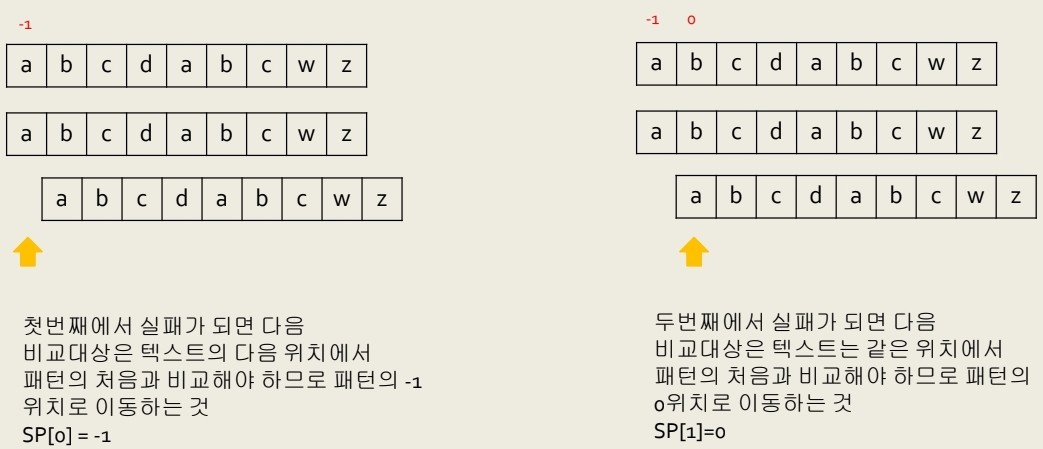
패턴 P 내에서 Prefix와 최대한 반복되는 부분을 찾아 기록하는게 포인트인데
위와 같이 초반부에는 보이지 않는다
계속 쭉 비교해본다
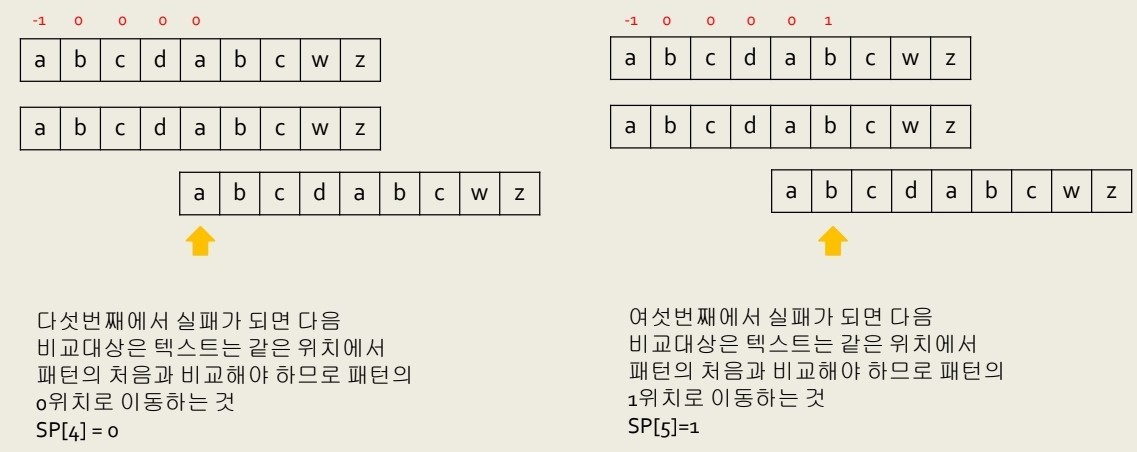
그러나 이렇게 6번째 인덱스에서 비교하면 앞에 "ab"까지는 같기때문에 여기서 틀리면
P의 Prefix "ab"와 같기에 다시처음부터 비교하는게 아닌
1번 index부터 확인하는게 효율적이다

그 후 이렇게 계속 비교해주면
불필요한 비교횟수를 줄여주면서 더 효율적인
알고리즘을 구성하게 된다!!
Boyer-Moore Algorithm
이 알고리즘은 조금 다르게
패턴 P를 앞으로 부터 아닌 뒤 문자들 부터 비교를 한다 (오른쪽)


문자열 매칭 문제에서는 또 활용할 수 있는 중요한 개념이 Suffix Array 이다
Suffix Array
S=banana
S 가 위 처럼 주워졌다 하자
0: banana
1: anana
2: nana
3: ana
4: na
5: a
그럼 suffix들의 index를 위와 같이 줄 수 있다
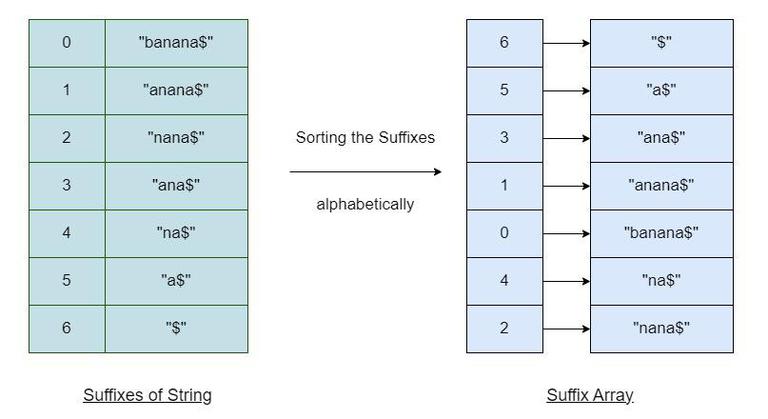
이제 이것을 사전순 (lexicographically) 으로 정렬 할 수 있는데
그러면 아래처럼 정렬되는데
5: a
3: ana
1: anana
0: banana
4: na
2: nana
그래서 S의 suffix array는 아래와 같다
S_sa=[5, 3, 1, 0, 4, 2]
특별한 알고리즘 없이 Naive하게 정렬해서 Suffix Array를 구축한다면
sort→O(nlogn)→comparison for each step →O(n)
그래서 새로운 알고리즘으로 구축하는데
Manber-Myers Algorithm
- Manber-Myers 알고리즘의 기본 아이디어
- 기존의 접미사 배열 구축 알고리즘들은 O(n^2*log n) 또는 O(n*log^2 n) 시간이 걸린다.
- Manber-Myers 알고리즘은 이를 O(n*log n)으로 개선했습니다.
- 핵심 아이디어: 접미사들을 2의 거듭제곱 길이씩 증가하면서 순차적으로 정렬한다.
- 알고리즘의 주요 구성 요소
- 배열 P: P[k][i]는 i번째 위치에서 시작하는 접미사의 첫 2^k문자를 기준으로 한 순위를 저장한다
- 초기화: P[0][i]는 첫 문자(또는 고정된 초기 순위 방법)를 기준으로 순위를 매긴다. 주로 ASCII 값을 사용
- 예제를 통한 알고리즘 이해
- 문자열 S = "banana"로 예시
- 각 위치의 문자: 'b', 'a', 'n', 'a', 'n', 'a'
- 순위 부여: P[0] = [1, 0, 2, 0, 2, 0]
- 페어 구성: [(1,0), (0,2), (2,0), (0,2), (2,0), (0,-1)]
- 예: (1,0)은 'ba'를 나타내며, 1은 'b'의 순위, 0은 'a'의 순위이다
- 페어 정렬: [(0,2), (0,2), (0,-1), (1,0), (2,0), (2,0)]
- 새 순위 부여: P[1] = [3, 0, 4, 1, 5, 2]
- 페어 구성: [(3,4), (0,5), (4,2), (1,-1), (5,-1), (2,-1)]
- 예: (3,4)는 'bana'를 나타내며, 3은 'ba'의 순위, 4는 'na'의 순위이다
- 페어 정렬: [(0,5), (1,-1), (2,-1), (3,4), (4,2), (5,-1)]
- 새 순위 부여: P[2] = [5, 0, 3, 1, 4, 2]
- 2^k가 문자열 전체를 커버할 때까지 과정을 반복
- 알고리즘의 장점
- 시간 복잡도: O(n*log n). 각 단계에서 O(n) 시간이 소요되며, 최대 log n단계가 필요하다
- 공간 복잡도: O(n). 추가 메모리 공간이 크게 필요하지 않는다.
- 안정성: 정렬 과정이 안정적이어서, 같은 순위의 접미사들의 상대적 순서가 유지된다
Suffix Tree
Tree 구조의 Suffix Tree인데 아래 조건들을 만족한다
1. 각 internal노드들은 자식이 최소 2개있다
2. n개의 leaf node들이 있다

ex)
S=”ATCACATCATCA”
- first find the longest common prefix of all the suffixes→here TCA
- then split into “A”, “CA”, and “TCA”
- repeat!
그래서 문자열T를 위한 Suffix tree는 O(n) 시간에 구축 가능하고 패턴P를 search하는데 O(m)이 걸린다

https://tonnykang.tistory.com/227
A* 알고리즘 (Dijkstra algorithm)
A* 알고리즘: 효율적인 경로 탐색을 위한 휴리스틱 기법 A* 알고리즘은 그래프에서 출발점부터 목표점까지의 최단 경로를 찾는 데 사용되는 휴리스틱 탐색 알고리즘이다.이 알고리즘은 Edsger W.
tonnykang.tistory.com
'컴퓨터공학 > 알고리즘' 카테고리의 다른 글
| NP, P, NP Complete, NP Hard problems 알고리즘 (29) | 2024.06.10 |
|---|---|
| Convex Hull Problem 컨벡스 헐 (35) | 2024.06.09 |
| A* 알고리즘 (Dijkstra algorithm) (23) | 2024.06.06 |
| Branch and Bound 분기 한정 알고리즘 (37) | 2024.06.05 |
| Back Tracking 백트래킹 알고리즘 (40) | 2024.06.03 |