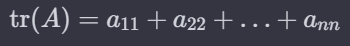행렬의 Trace는 그 행렬의 대각 성분들의 합이다 (좌측 상단 부터 우측 하단) N x N 크기의 정방 행렬이 있다면 그 행렬의 trace는 아래와 같이 정의 된다 그래서 trace는 행렬의 대각 성분들의 합으로 계산되어 스칼라 값이 됩니다. 행렬의 트레이스(trace)는 선형 대수학 및 기타 수학 분야에서 여러 흥미로운 성질과 응용을 가지고 있습니다. 예를 들어, 유사 변환(similarity transformations) 하에서 불변하며(변하지 않음), 행렬의 고유값(eigenvalues)의 합과 동일합니다. 물리학에서는 트레이스가 종종 에너지-운동량 텐서(energy-momentum tensor)의 식에서 나타납니다. For a 2x2 matrix: For a 3x3 matr..