반응형
🎲 주요 확률분포들의 정리
📏 균등 분포 (Uniform Distribution)
📌 확률 밀도 함수 (PDF)
a부터 b까지 일정한 확률을 가지는 균등 분포:
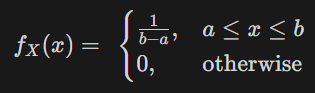
📌 누적 분포 함수 (CDF)
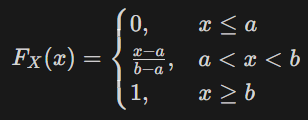
🔔 정규 분포 (Normal Distribution)
📌 확률 밀도 함수 (PDF)
728x90
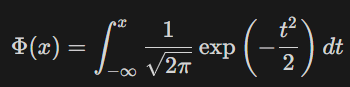
샘플 수 N이 충분히 크면, X의 평균은 정규 분포를 따른다 (중심극한정리).
Central Limit Theory
📌 표준 정규 분포 (Standard Gaussian)
평균이 0이고 분산이 1인 경우, 이를 표준 정규 분포라고 한다.

일반적인 X는 다음과 같이 표준화할 수 있다:

📊 카이제곱 분포 (Chi-squared Distribution)
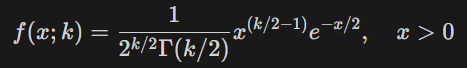
- x: 확률을 평가하는 값
- k: 자유도
- Γ: 감마 함수 (팩토리얼의 일반화)
⏳ 지수 분포 (Exponential Distribution)
📌 확률 밀도 함수 (PDF)
반응형

- β > 0
- 어떤 사건까지의 대기 시간(예: 전자 부품의 수명 등)을 모델링할 때 사용
🪙 베르누이 분포 (Bernoulli Distribution)
X는 동전 던지기의 결과를 나타냄 (성공 또는 실패)
📌 확률 질량 함수 (PMF)

📌 누적 분포 함수 (CDF)
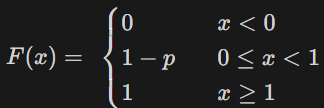
📌 기대값과 분산
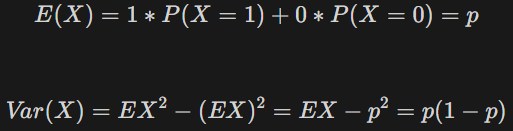
🪙 이항 분포 (Binomial Distribution)
동전을 nn번 던졌을 때, 앞면이 나오는 횟수를 X라고 하자.
📌 확률 질량 함수 (PMF)
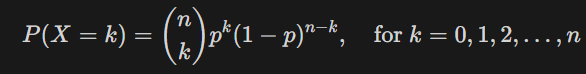
🔢 포아송 분포 (Poisson Distribution)
일정한 시간이나 공간 내에서 사건이 발생하는 횟수를 모델링할 때 사용
예시:
하와이에서 1년 동안 화산 폭발 횟수
아침에 맥도날드에 도착하는 고객 수
📌 확률 질량 함수 (PMF)
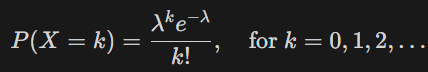
반응형
'컴퓨터공학 > 확률과 통계' 카테고리의 다른 글
| 확률 분포 Probability Distributions (0) | 2025.04.15 |
|---|