데이터베이스 SQL문도 공부하느라 정신 없는데 설계이론 까지 공부해야하느냐?
아래 시나리오들을 살펴보자
다음은 제대로 설계되지 못한 데이터베이스의 예시이다

위와 같이 Student, Course, Room 이 있는 테이블이 있다 하자
예시에는 한개의 수업만 있지만
여러수업이 있고 여러수업이 다 한 강의실에서 강의를 하면
Redundant Storage, 쓸모 없는 저장 공간을 차지하게 된다
Update Anomaly

수업 한개의 강의실 하나를 업데이트하면 Inconsistent 한 Data를 가지게 된다
Insert Anomaly

또한 한 강의에 대한 정보를 입력하려하는데
위와 같이 Student에 데이터가 없으면 테이블에 Tuple을 추가할 수가 없다.
Delete Anomaly

한 강의에 또한, 모든 학생들이 드랍 하면 그 강의에 대한 정보를 찾을 수 없다, 영영...
그러면 뭐 어쩌란 말이냐?
데이터베이스를 분해할 필요가 있다!
Decomposition

Functonal Dependencies
FD라고 부르기도 하는데
Constraint의 한 형태이다
A -> B 라고 표기하며 뜻은 "어느 두 투플이 A에 대해 일치하면, B도 일치함을 보장한다" 이다
(A와 B는 Attribute들의 집합)
Ex)
StudentID -> Name
좀더 정식적으로 정의하면, A가 아래와 같이 주어지고

B는 다음과 같을 때

A -> B의 Functional Dependency는 두 tuple t1과 t2에 대해
IF
t1[A1] = t2[A1], t1[A2]=t2[A2], … , t1[Am]=t2[Am]
THEN
t1[B1] = t2[B1], t1[B2]=t2[B2], … , t1[Bm]=t2[m]

FD를 찾아내기
FD는 Domain 지식이다, 단순히 튜플 몇개만 봐서 파악가능한 것이 아니다
그래서 튜플의 집합 (테이블, 릴레이션)이 주어지면, 우리는 "유효하다" 라고만 말할 수 있고 전체 데이터베이스 구조에 해당됨을 증명 할 수 없다
ER and FD

좋은 FD와 나쁜 FD
좋은 FD:
- 중복 데이터를 최소화
- 이상치의 확률을 줄임
나쁜 FD:
- 중복 데이터 존재
- 데이터 이상치 존재
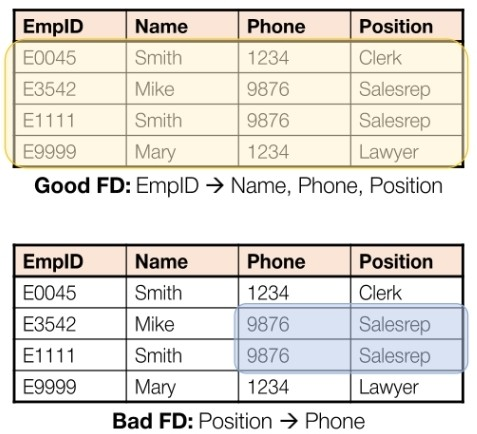
굳이 좋고 나쁜 FD를 정의까지 했으니
우리는 모든 FD를 추려내서 나쁜 FD를 없에고 싶은게 목표이다
그러나 FD는 한 데이터 베이스에 굉장히 많을 수 있다
아니, 웬만하면 많다
Armstrong's Axioms
Reflexivity
어느 부분집합

에 대해서

Ex)
A,B → B
A, B, C → A, B
A, B, C → A, B, C
Augmentation
어떤 attribute의 집합 X,Y,Z에 대해서
if X → Y then X,Z → Y,Z

Ex)
A→B implies A,C → B,C
A,B → C implies A,B,C → C
Transitivity
어떤 attribute의 집합 X,Y,Z에 대해서
if X → Y and Y → Z then X → Z

Ex)
A → B and B → C imply A → C
A → C, D and C, D → E imly A → E
추가 Rule들
Union Rule: If A → B and A → C, then A → B,C
Decomposition Rule: If A → B,C then A → B and A → C
Pseudotransitivity Rule: If A → B and B, C → D, then A, C → D
Closure of a set of FDs
F가 FD들의 집합이면 , F의 closure은

로 표기한다
F로부터 논리적으로 추론된 FD들의 집합이다
Closure of a set of Attributes
위와 같은 규칙들을 활용해 attribute X에서 추론할 수 있는 닫힌 attribute를

라고 표기하면
The closure of a set of attributes라고 한다
Closure Algorithm
처음 주어진 attributes X와 FD의 집합인 F를 가지고 시작한다
다음을 X가 변하지 않을 때 까지 반복한다:
X의 부분집합인 B에 대해, B->C가 FD이면 X에 원소 C를 추가해라
그래서 X가 정적이게 되면 X가 the closure of the set of attributes 이다

이번은 FD를 위한 Closure 알고리즘은
위와 같이 attribute에 대한 closure을 찾은 후
1. 각 X+의 부분집합 X에 대해서, Closure 알고리즘을 수행한다
2. 앞 단계에서 계산된 Closure들의 부분집합 Y에 대해서 , X->Y라는 FD를 추출한다

Key 와 Superkey
Superkey는 attribute들의 집합이며

를 만족한다
그리고 minimal한 superkey는 key라고 한다

한 relation내에 여러 key가 존재 할 수 있다
Ex)
R(A, B, C)
F: A,B →C
A,C →B
both {A,B}, {A,C} are keys
FD 분해하기
FD: A,B -> C,D 를 한번 보면
오른쪽 C와 D는 A,B에 의해 독립적으로 determined되는 관계이다
그래서 위 FD를
A, B -> C와 A,B -> D로 분해할 수 있다
하지만 좌측에 대해서는 똑같은 분해를 할 수 없다
FD의 Minimal Basis
FD의 minimal Basis는 Closure Set의 반대이다
구하려면
1. FD의 우측을 분해한다
2. 좌측을 정리한다, 필요 없는 attribute는 삭제
3. 필요없는 FD들은 정리한다


'컴퓨터공학 > 데이터베이스 DB' 카테고리의 다른 글
| 데이터 베이스 정규화 Normalization (2) | 2025.01.01 |
|---|---|
| 데이터 베이스 권한 Authorization (2) | 2024.12.28 |
| 데이터베이스 Transaction 트랜잭션 (2) | 2024.12.27 |
| 데이터베이스 제약조건 Integrity Constraints (3) | 2024.12.26 |
| 데이터베이스 뷰 View (3) | 2024.12.25 |