거리 측도
변수가 연속형인 경우
유클리디안 거리 (Euclidean):
L2 Norm, 두 점 사이의 거리를 계산할 때 가장 널리 쓰이는 계산 방법으로, 두 점 사이의 가장 짧은 거리를 계산한다
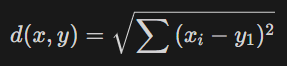
맨하튼 거리 (Manhattan):
L1 Norm, 두 점 사이를 가로지르지 않고 길을 따라 갔을 때의 거리고, 변수들의 차이의 단순합으로 계산한 거리다


체비셰프 거리 (Chebyshev):
변수 간 거리 차이 중 최대값을 데이터 간의 거리로 정의한다.

마할라노비스 거리:
표준화 거리가 고려하지 못한 변수 간 상관성까지 고려한 거리다

(S:변수의 공분산을 성분으로 하는 대각행렬)
민코프스키 거리:
Generalized Norm, 유클리디안 거리와 맨하튼 거리를 한번에 표현한 거리로, m=1일 때는 맨하튼 거리이며, m=2일 때는 유클리디안 거리가 된다

변수가 범주형인 경우
단순 일치 계수:
Simple Matching Coefficient, 두 객체 i와 j간의 상이성을 불일치 비율로 계산한다, P는 변수의 총 개수이며, m은 객체 i와 j가 같은 상태인 변수의 수를 의미한다

자카드 지수:
두 집합 사이의 유사도를 측정하는 지표로서 두 집합이 같으며 1, 완전히 다르면 0 의 값을 같는다

자카드 거리:
자카드 지수를 거리화하기 위해 완전히 다르면 먼 거리를 갖는 1로, 완전히 동일하면 거리를 0으로 변환하기 위해 1에서 자카드 지수를 뺀 값이다

코사인 유사도:
방향성을 측정하는 지표다, 완전히 일치하면 1의 값을 가지며, 완전히 다른 방향이면 -1의 값을 갖는다

코사인 거리:
코사인 유사도를 거리화하기 위해 1에서 코사인 유사도를 뺸 값이다

군집 간의 거리
단일연결법 (Single Linkage)
최단연결법이라고도 하며 생성된 군집과 기존의 데이터들의 거리를 가장 가까운 데이터로 계산하는 방법이다
완전연결법 (Complete Linkage)
최장연결법이라고도 하며 생성된 군집과 기존의 데이터들의 거리를 가장 먼 데이터로 계산하는 방법이다
평균연결법 (Average Linkage)
생성된 군집과 기존의 데이터들의 거리를 군집 내 평균 데이터로 계산하는 방법이다
이상치에 덜 민감하다
중심연결법 (Centroid Linkage)
각 군집의 중심점 사이의 거리를 거리로 정의한 방법이다, 평균연결법보다 계산량이 적다
와드연결법 (Ward Linkage)
생성된 군집과 기존의 데이터들의 거리를 군집 내 오차가 최소가 되는 데이터로 계산하는 방법이다
오차=Variance
K-Means 군집 Clustering
- 군집의 수 K개를 사전에 정한 뒤 집단 내 동질성과 집단 간 이질성이 모두 높게 전체 데이터를 k개의 군집으로 분할하는 알고리즘이다
- 군집의 수 k의 초기값을 설정하고 각각의 k를 설명할 변수의 값을 임의로 설정하거나 데이터 중에서 k개를 선택한다, 이때 임의로 설정한 k개의 데이터를 seed라고 한다
'컴퓨터공학 > ADsP' 카테고리의 다른 글
| ADSP 전공자의 독학 후기 (10) | 2024.11.07 |
|---|---|
| ADsP 데이터 분석 준 전문가 정리 18 (39) | 2024.07.26 |
| ADsP 데이터 분석 준 전문가 정리 16 (46) | 2024.07.22 |
| ADsP 데이터 분석 준 전문가 정리 15 (56) | 2024.07.21 |
| ADsP 데이터 분석 준 전문가 정리 14 (37) | 2024.07.20 |