우리는 흔히 '더 많이', '더 좋게'가 항상 긍정적인 결과를 가져올 것이라고 생각합니다. 하지만 현실은 그리 단순하지 않죠. 때로는 무언가를 추가하는 것이 오히려 전체 시스템의 성능을 저하시키고, 핵심 요소를 제거하는 것이 더 나은 결과를 가져올 수 있습니다. 이러한 역설적인 상황을 잘 보여주는 두 가지 흥미로운 현상이 바로 Braess' Paradox와 Ewing Paradox입니다.
Braess' Paradox: 더하기가 때론 빼기다
Braess' Paradox는 1968년 독일의 수학자 Dietrich Braess가 발견한 현상입니다. 이 역설은 교통 네트워크에서 새로운 도로를 추가했을 때 오히려 전체적인 교통 흐름이 악화될 수 있다는 것을 보여줍니다.
마치 Game Theory 와 비슷합니다
예를 들어 봅시다:
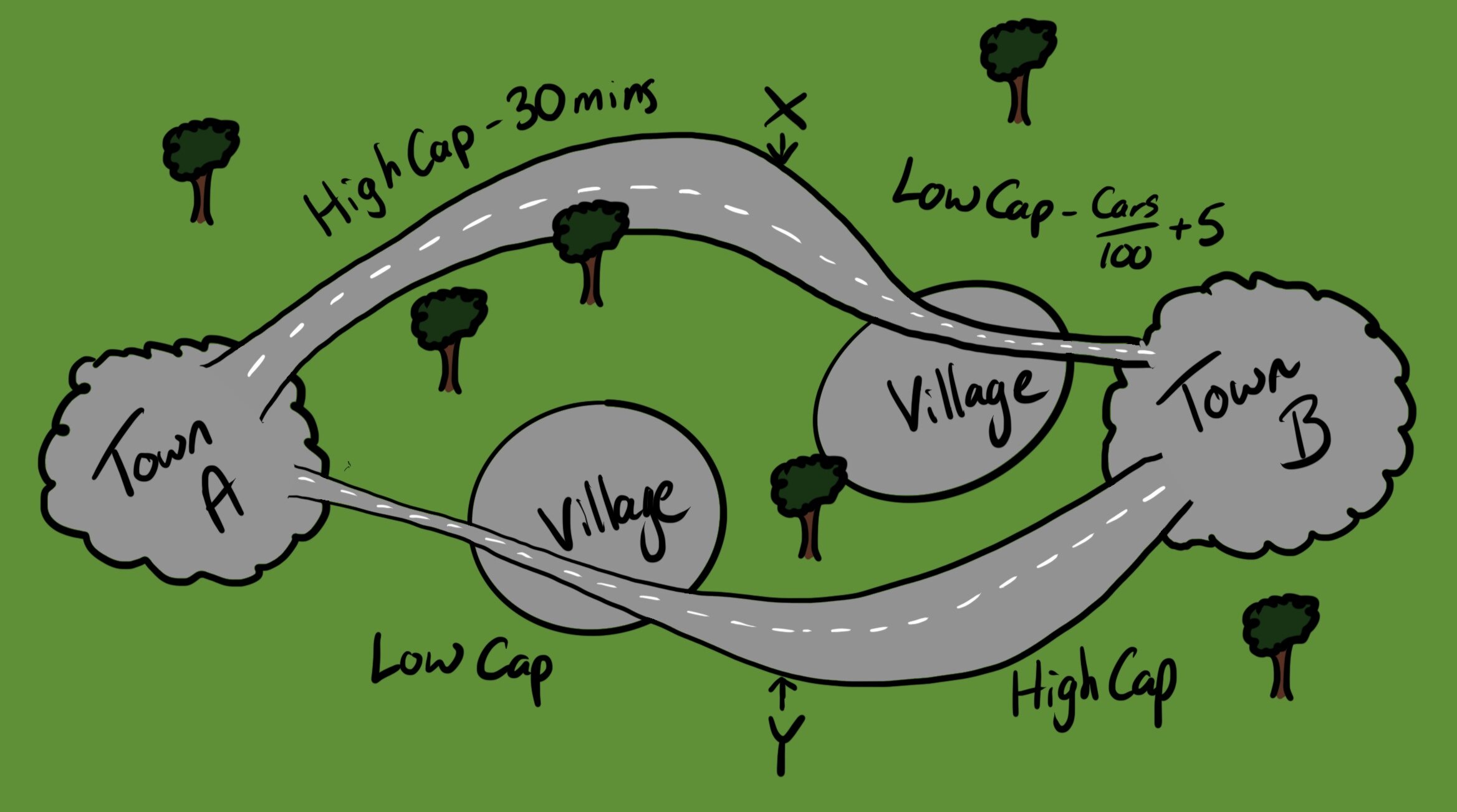
- 도시 A와 B 사이에 두 개의 주요 도로가 있다고 가정해봅시다.
- 두 도로 모두 혼잡할 때 30분, 한산할 때 10분이 걸립니다.
- 현재 상황에서 운전자들은 균형 있게 두 도로를 이용하고 있어, 모두가 20분씩 소요됩니다.
여기서 도시 정부가 A와 B를 잇는 새로운 지름길을 만들었다고 해봅시다. 이 새 도로는 항상 5분이 걸립니다. 얼핏 보기에 이는 훌륭한 해결책처럼 보입니다. 하지만 결과는 어떨까요?
- 많은 운전자들이 이 새 도로를 이용하려 할 것입니다.
- 이로 인해 기존 도로들은 한산해지고, 새 도로로 향하는 경로는 혼잡해집니다.
- 결과적으로 모든 운전자의 이동 시간이 25분으로 증가하게 됩니다.
이처럼 Braess' Paradox는 개인의 최적화가 반드시 전체의 최적화로 이어지지 않는다는 점을 보여줍니다. 때로는 시스템에 새로운 요소를 추가하는 것이 오히려 전체 성능을 저하시킬 수 있는 것이죠.

Ewing Theory: 스타 선수의 부재가 전화위복이 되는 경우
-유잉 무용론
이제 스포츠 세계로 눈을 돌려봅시다. Ewing Theory는 NBA의 전설적인 선수 Patrick Ewing의 이름을 따서 명명되었습니다. 이 역설은 팀의 핵심 선수가 결장했을 때 오히려 팀의 성적이 좋아지는 현상을 말합니다.
|
뉴욕 닉스 No. 33
|
|
|
패트릭 앨로이셔스 유잉
Patrick Aloysius Ewing |
|
|
출생
|
|
|
국적
|
|
|
출신학교
|
|
|
신장
|
213cm (7' 0")[1]
|
|
체중
|
116kg (255 lbs)[2]
|
|
윙스팬
|
244cm (8' 0", 비공식)[3]
|
|
포지션
|
|
|
드래프트
|
|
|
소속 팀
|
|
|
지도자
|
워싱턴 위저즈 코치 (2002~2003)
휴스턴 로키츠 코치 (2003~2006) 올랜도 매직 코치 (2007~2012) 샬럿 밥캣츠-호네츠 코치 (2013~2017) 조지타운 대학교 감독 (2017~2023) |
|
등번호
|
|
Patrick Ewing이 뉴욕 닉스에서 활약하던 시절, 그가 부상으로 결장한 경기에서 팀이 더 좋은 성적을 거두는 경우가 종종 있었습니다.
이 이론의 탄생 배경에는 1999년 NBA 플레이오프, 특히 동부 컨퍼런스 파이널이 있습니다.
당시 뉴욕 닉스와 인디애나 페이서스의 경기에서 흥미로운 일이 벌어졌습니다.
Patrick Ewing이 부상으로 빠진 3, 4차전에서 닉스가 승리를 거둔 반면, Ewing이 출전한 1, 2, 5, 6차전에서는 모두 패배한 것입니다.
이 사건은 Ewing의 실제 경기 기여도에 대한 의문을 불러일으켰습니다.
Ewing은 뛰어난 개인 기록을 가진 선수였지만, 실제 경기에서의 영향력은 그에 미치지 못했다는 주장이 제기되었습니다.

이는 어떻게 설명할 수 있을까요?
- 스타 선수에 대한 과도한 의존: 팀이 한 선수에게 지나치게 의존할 경우, 그 선수가 없을 때 오히려 더 균형 잡힌 플레이가 가능할 수 있습니다.

- 다른 선수들의 성장 기회: 주요 선수의 부재는 다른 선수들이 자신의 능력을 발휘할 기회를 제공합니다.
- 상대팀의 전략 변화: 핵심 선수가 없을 때 상대팀이 방심하거나 전략을 잘못 세울 수 있습니다.
Ewing Theory는 팀 스포츠에서
전체는 부분의 합보다 크다
라는 격언을 잘 보여줍니다. 때로는 가장 뛰어난 개인을 제외하는 것이 전체 팀의 성과를 향상시킬 수 있는 것입니다.
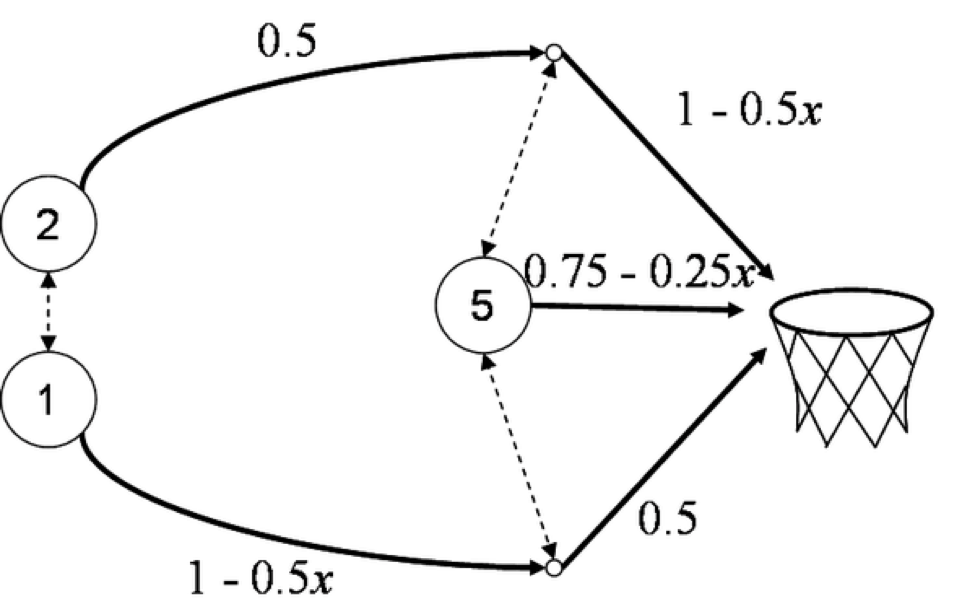
위와 같이
point guard (1), the shooting guard (2), and the center (5)
선수들이 3명 있다
여기서 1번 2번 선수는 각각 돌파 할 수 있으며
돌파 후 직접 슈팅을 가져가거나 센터에게 패스를 할 수 있다
여기서 x는 1번의 돌파가 하느냐 안하느냐를 나타낸 변수이다
x는 그 단계를 얼마나 자주 택하는가이다
예를들어 1이 돌파를 항상하면 x=1
수비가 그를 예측하기 마련이다
그래서 성공률은
1-0.5*1=0.5 이다
절대로 돌파안하면 x=0
성공률은
1-0.5*0=1이고
반반이면 x=0.5로
성공률이
1-0.5*0.5 = 0.75이다
x는 0.25같은 숫자일 수도 있다
그럼 위와같은 경우에서는 (2) 슈팅 가드의 돌파 확률은 (1) 포인트 가드의 돌파 성공률보다 높을 수가 없다
그래서 위의 노드는 사용되지 않는다
또한 포인트가드의 슈팅 성공률은 다른 두 선수보다 더 높을 수 없음으로 슈팅을 안하게 된다
In order to determine the Nash Equilibrium, we set 0.75-0.25x = 1 – 0.5(1-x), where x represents the fraction of times that the center shoots. This works out to x = 1/3, so the center takes the shot 1/3 of the time, while the center passes to the shooting guard who takes the layup 2/3 of the time. Since the shooting is successful 2/3 of the time and the driving is successful 1/2 of the time, the overall success rate of the play is 1/3.
->대충 성공률 33%정도 된다는 뜻
여기서 센터가 없다면 어떻게 될까?

센터가 없으면 더 못할 것 같다고 예상되지만
여기서는 nash equilibrium에서 x=0.5이기에 37.5%의 더 높은 성공률이 나오게된다