Genetic Algorithm 유전 알고리즘
유전 알고리즘(Genetic Algorithm, GA)
자연세계의 진화과정 및 유전법칙에 기초한 계산 모델로서 존 홀랜드(John Holland)에 의해서 1975년에 개발된 전역 최적화 기법(Global Optimization Method)
생물의 진화를 모방한 진화 연산의 대표적인 기법으로, 실제 진화의 과정에서 많은 부분을 차용하였으며, 변이(돌연변이), 교배 연산, 세대, 인구 등의 개념을 문제 풀이 과정에서 사용
문제가 계산 불가능할 정도로 지나치게 복잡할 경우 유전 알고리즘을 통하여, 실제 최적해를 구하지는 못하더라도 최적해에 가까운 답을 얻을 수 있음
아래는 전반적인 GA의 과정이다
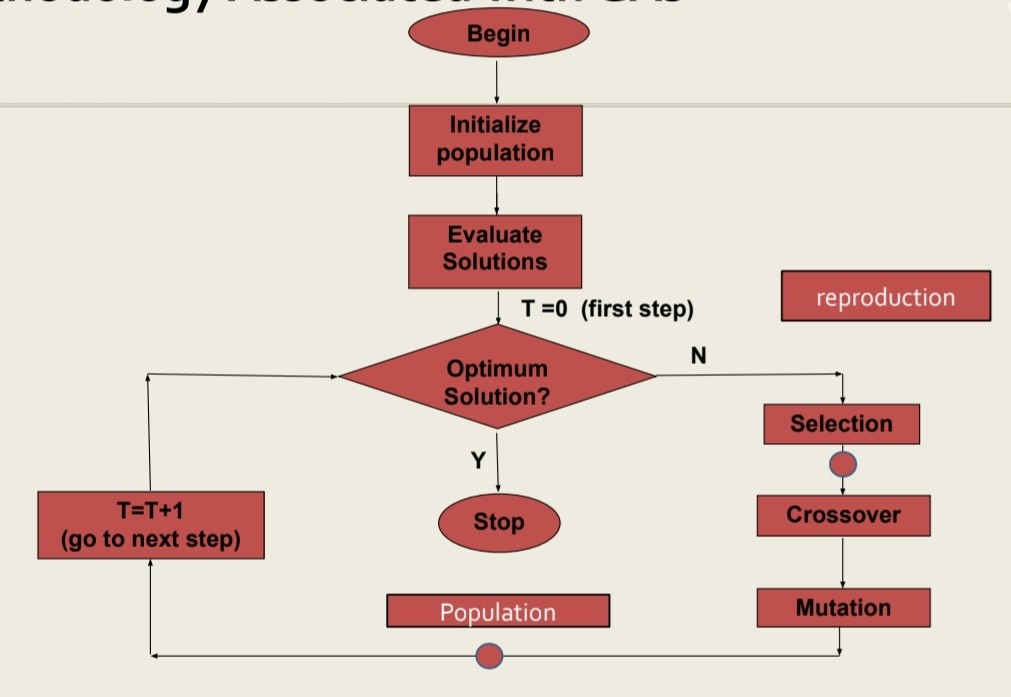
Starts with a population of individuals (다수의 개별 솔루션으로 시작)
Each individual (state=솔루션) is represented as a string over a finite alphabet (called chromosome, 염색체)
—가장 흔하게는, a string of 0s and 1s (binary)
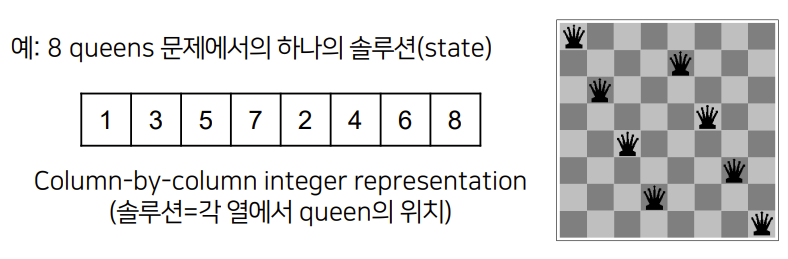
이런 solution을 나타내는 방법이 여러가지 있는데
이 방법들을 Encoding이라고 한다
bit strings : {010101010101}
real numbers: {23.4, 453.2, 123.,12}
permutations of an elements →the cities to visit in TSP
list of rules: {R1, R2, R3…}
value coding: {(left), (back), (left), (right), (forward)}
정보를 문자열로 저장할 수만 있다면 그 어떠한 자료구조이건 상관없다
하지만 GA의 Performance에 가장 큰 영향을 끼치는건 바로
Fitness Function
Each individual is rated by the fitness function (적합도 함수에 따라 각 솔루션이 평가됨)
Fitness 값에 따라 솔루션을 선택하며, 선택된 솔루션을 사용하여 자손을 생성함
(자 손 = next solution, 자손 생성 = reproduction)
fitness function은 Objective Function의 일종으로
한 solution이 다른 solution보다 낫다는 척도가 되고
또한 GA알고리즘의 종료도
Fitness Function점수가 어느정도 충족됐을떄 종료된다
Fitness Function vs Objective Function
- In a genetic algorithm trying to maximize a function f(x), the fitness function could be fitness(x)=f(x).fitness(x)=f(x)
- f(x)f(x)
- For minimization problems, the fitness function might transform the objective function to make higher fitness values better, such as fitness(x)=1+f(x)1.
- fitness(x)=1/(1 + f(x))
Crossover
Selected pair are mated (짝짓기) by a crossover (교차 연산)
한 쌍의 염색체(=솔루션)를 선택한 후, 둘을 랜덤하게 잘라서 엇갈리게 이어 붙이는 ‘교차 연산‘ 방식으로 새로운 솔루션을 생성함

Crossover하는 방법도 여러가지가 있다
Uniform Crossover: through a mask {0,1,1,1,0,0,0,1} 0: don’t 1: switch
single-point crossover: split the solutions to two areas {keep|switch} ->반반으로 나뉨

two point crossover: three areas {keep|switch|keep} or {switch|keep|switch} ->3개의 영역으로 나뉨
uniform crossover: no solid areas
Crossover은 항상 더 나은 solution을 보장하지는 않는다!
좋은 부모(솔루션) -> 좋은 자식(솔루션) 가능성이 높음
이러한 연산은 Local Minimum 값에 빠지지 않게 도와주며
기존 Population에 있던 solution들의 성장을 가능하게 한다
Algorithm 초반에는 Crossover을 많이 시키고
후반부에는 적게 시키는 편이다
Mutation
Crossover 이후에 돌연변이(mutation) 연산을 적용함
염색체(솔루션) 자리 하나 하나에 대해서, 작은 확률로 무작위로 변경함
TSP같은 문제에 많이 사용되는 방법이 Inversion이다

Range안에 있는 문자열의 순서를 뒤집는 방법이다
Elitism
Crossover, Mutation연산을 하기 전에
이미 너무나 좋은 solution이 Population에 있으면
위와같은 연산으로 좋은 solution을 잃을 수 있기에
미리 빼놓고 Crossover, Mutation을 시행하는 방법이다
GA알고리즘은
언젠가 해답을 찾는 특징이 있으며 시간이 지날 수록 solution이 더 좋아진다
하지만 성능은 Fitness Function에 크게 달려 있으며, 전반적인 성능이 다른 특화된 알고리즘을 뛰어넘기는 힘들다
예시

(a) 임의로 선택된 다수의 솔루션으로 시작 (initial population)
(b) 선택된 솔루션에 대해 적합도를 계산 (fitness score)
(c) 각 솔루션은 적합도 함수 값에 비례하는 확률로 선택됨
(d) 두 개의 솔루션을 선택하고, 임의의 위치를 기준으로 두 솔루션을 교차로 합쳐서 새로운 솔루션 생성 (crossover)
(e) 생성된 솔루션 각각에 대해 임의의 위치에서 무작위로 솔루션을 변형 (mutation)함. 단, 확률에 따라 진행되므로, mutation이 적용되지 않는다
PseudoCode
function GENETIC-ALGORITHM(population, FITNESS-FN) returns an individual
inputs: population, a set of individuals
FITNESS-FN, a function that measures the fitness of an individual
repeat
new_population ← empty set
for i = 1 to SIZE(population) do
(x, y) ← SELECT-PARENTS(population, FITNESS-FN)
child ← REPRODUCE(x, y)
if (small random probability) then child ← MUTATE(child)
add child to new_population
population ← new_population
until some individual is fit enough, or enough time has elapsed
return the best individual in population, according to FITNESS-FN