정렬된 배열을 위한 효율적인 해법: Binary Search (이진탐색)
Binary Search는 정렬된 배열 내에서 대상 요소를 효율적으로 검색할 수 있는 강력한 알고리즘입니다. 이 알고리즘은 검색 공간을 반복적으로 절반씩 나누는 방식으로 작동하므로, 큰 규모의 정렬된 데이터셋에서도 매우 빠르게 동작합니다.
전제 조건: 정렬된 배열
Binary Search를 사용하기 위해서는 배열이 사전에 정렬되어 있어야 합니다. 배열이 정렬되어 있지 않다면 Binary Search가 올바르게 작동하지 않으며, 잘못된 결과를 얻을 수 있습니다.
이러한 요구 사항이 필요한 이유는 Binary Search가 배열의 정렬 순서에 의존하기 때문입니다. 이를 통해 알고리즘은 현재 검색 공간의 중간 요소와 대상 요소를 비교하여 다음에 검색할 절반을 결정할 수 있습니다.
그래서 Sorting이 중요함!
Binary Search 알고리즘
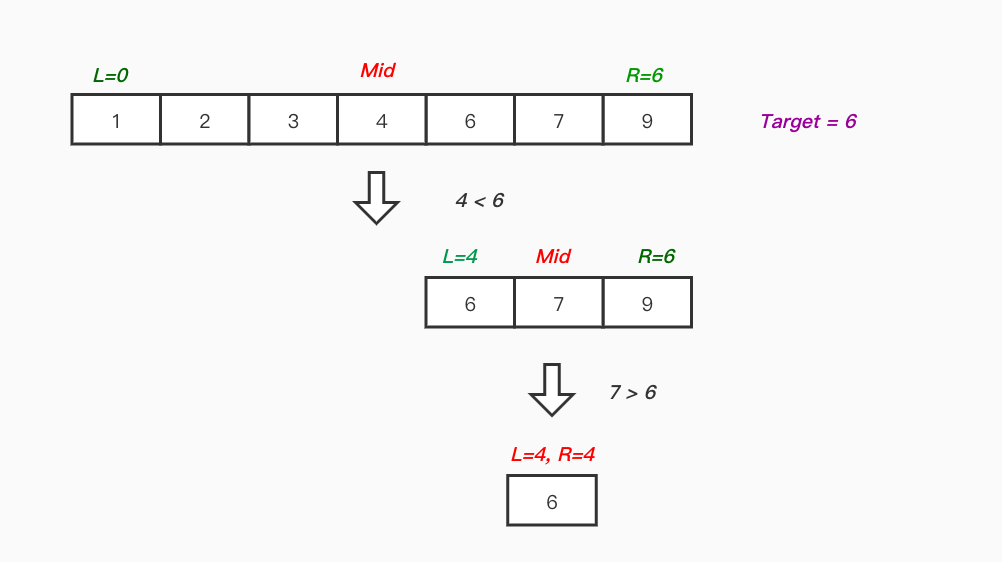
Binary Search 알고리즘은 다음과 같은 단계를 따릅니다:
1. 검색 공간 초기화: 배열의 첫 번째 인덱스를 하한(left)으로, 마지막 인덱스를 상한(right)으로 설정합니다.
2. 대상을 찾을 때까지 또는 검색 공간이 비워질 때까지 다음 단계를 반복합니다:
- 중간 인덱스 계산: `mid = (left + right) / 2`
- 중간 요소와 대상 비교:
- 중간 요소가 대상과 같으면 중간 인덱스를 반환합니다.
- 중간 요소가 대상보다 작으면 하한을 `mid + 1`로 업데이트합니다(오른쪽 절반 검색).
- 중간 요소가 대상보다 크면 상한을 `mid - 1`로 업데이트합니다(왼쪽 절반 검색).
3. 대상을 찾지 못한 경우 -1(또는 적절한 오류 메시지)을 반환합니다.
예시를 통해 프로세스를 더 잘 이해해 보겠습니다:
정렬된 배열 `arr = [1, 3, 5, 7, 9, 11, 13]`에서 대상 요소 `7`의 인덱스를 찾아봅시다.
1. 검색 공간 초기화: `left = 0`, `right = 6`.
2. 중간 인덱스 계산: `mid = (0 + 6) / 2 = 3`.
3. 중간 요소(`arr[3] = 7`)와 대상(7)을 비교합니다. 두 값이 같으므로 중간 인덱스 3을 반환합니다.
Binary Search의 시간 복잡도
Binary Search의 시간 복잡도는 O(log n)입니다. 여기서 n은 배열의 크기를 나타냅니다. 이는 대상 요소를 찾거나(또는 없다는 것을 알아내는 데) 걸리는 시간이 배열 크기의 로그에 비례하여 증가한다는 의미입니다.
이렇게 효율적인 시간 복잡도를 가지는 이유는 알고리즘의 각 반복 단계에서 검색 공간이 절반으로 줄어들기 때문입니다. 이를 통해 알고리즘은 큰 규모의 정렬된 배열에서도 빠르게 대상 요소에 수렴할 수 있습니다.
반면, 정렬되지 않은 배열에 대한 단순한 선형 검색의 시간 복잡도는 O(n)이며, 큰 데이터셋에서는 훨씬 더 느릴 수 있습니다.
Python 예제 코드
def binary_search(arr, target):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
# Example usage
sorted_arr = [1, 3, 5, 7, 9, 11, 13]
print(binary_search(sorted_arr, 7)) # Output: 3
print(binary_search(sorted_arr, 4)) # Output: -1
C++ 예제 코드
#include <iostream>
#include <vector>
int binarySearch(std::vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
int main() {
std::vector<int> sortedArr = {1, 3, 5, 7, 9, 11, 13};
std::cout << binarySearch(sortedArr, 7) << std::endl; // Output: 3
std::cout << binarySearch(sortedArr, 4) << std::endl; // Output: -1
return 0;
}
결론
Binary Search는 정렬된 배열 검색을 위한 매우 효율적인 알고리즘입니다. 검색 공간을 반복적으로 절반씩 나누는 방식을 통해 대상 요소를 빠르고 확장 가능한 방식으로 찾아낼 수 있습니다. 하지만 이 알고리즘은 데이터가 사전에 정렬되어 있어야 하므로, 정렬 과정이 선행되어야 합니다.