컴퓨터공학/알고리즘
Strassen Algorithm (스트라센 알고리즘) 행렬의 곱
Tonny Kang
2024. 3. 2. 08:57
반응형

위와같은 두 행렬들이 있다하자 그러면
행렬 A와B의 곲 C는 다음과 같이 표현된다

그러면 아래와같이 이해될 수 있다
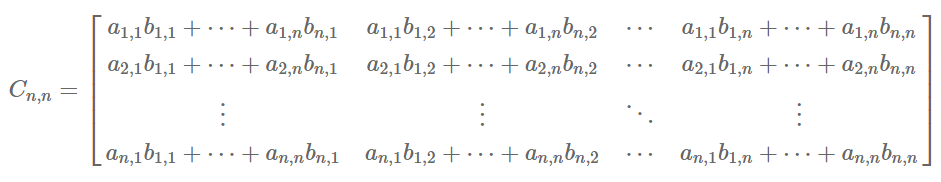
이 행렬의 곱 알고리즘의 시간 복잡도는
O(n^3)의 복잡도를 가진다
그래서 매우 큰 행렬들의 곱을 계산할 때는 매우 버거워진다
그의 결과로
분할정복의 한 방법인 Strassen 알고리즘이 나왔다

각 행렬들을 이렇게 4분할을 해보자

그러면 이렇게 계산해도 결과가 나온다
하지만 이건 또 결국 계산을 하다보면 O(n^3)의 복잡도를 가진다
그럼 Strassen 알고리즘은 어떻게 분할하냐?

위의 행렬들을 정의 해준다
그럼 아래와 같은 곱이 성립 한다
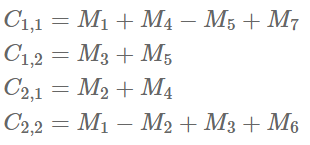
행렬의 곱셈을 한번 줄이고! 덧셈을 늘렸다!
그래서 O(n^3)->O(n^2) 로 수렴하게 된다
왜냐
행렬의 곱셈은 for문 골치거리이기 때문에
그러나
Strassen 알고리즘은 여러 행렬 덧셈을 수행하므로 매우 큰 이 아니면 사실 원래 하는 것 보다 더 오래 걸린다
big O notation은 더 빠를 수 있지만
이건 계수랑 밑에 하위항을 다 생략한 것이기 때문이다
그래서 더 큰 행렬을 계산 할 일이 생기면
Strassen Algorithm
반응형